ABC for blind
It is known that in books for the blind, different combinations of protrusions are used to designate different letters, which the reader distinguishes by touch [1]. Let a rectangle with a width of m mm and a height of n mm be used to denote a letter, and some squares of size 1 * 1 included in it contain a ledge.
Since the blind man does not see the borders of the rectangle, he cannot distinguish combinations obtained from each other by a shift. So, he cannot distinguish combinations a) and b) in the figure. (At the same time, combinations a) and c) are distinguishable, since they cannot be obtained from each other by a shift)
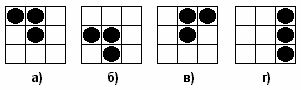
Because of this, when developing the alphabet for the blind, the problem arose: how many different letters can be represented using protrusions if it is forbidden to match different letters to combinations obtained from each other by a shift. A rectangle without protrusions at all can not be used as a letter (since when writing a word between some letters, such a rectangle may appear, for example, between a) and d) in the figure).
Count the number of different letters that can be represented in this way, if the rectangle has a size m * n.
As an example, all letters of size 2 * 2 are shown in the figure (among the combinations corresponding to one letter, only one is given).

[1] The model considered in the problem only approximately corresponds to reality.
Input
Two numbers m and n. Since a person cannot simultaneously receive too much information, then m * n ≤ 30.
Output
Print the number of different letters that the blind can distinguish at the given size of the rectangle.