Editorial

In the first box, you can place any of the $n$ balls. The color of the ball in the second box must differ from the color of the ball in the first box. Therefore, in the second box, you can place a ball of any of the remaining $n - 1$ colors. In the $i$ -th box, you can place a ball of any color that is different from the color of the ball in the $(i - 1)$ -th box.

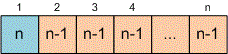
Thus, the number of different ways to arrange the balls in the boxes is equal to

n \cdot (n - 1)^{n - 1} m o d (1 0^{9} + 7)

Algorithm implementation

Let's define the modulus $MO D = 1 0^{9} + 7$ for the computations.

#define MOD 1000000007

The powmod function computes the value of $x^{n} m o d m$ .

long long powmod(long long x, long long n, long long m)
{
  if (n == 0) return 1;
  if (n % 2 == 0) return powmod((x * x) % m, n / 2, m);
  return (x * powmod(x, n - 1, m)) % m;
}

The main part of the program. Read the input value of $n$ .

scanf("%lld", &n);

Compute and print the answer.

res = (powmod(n - 1, n - 1, MOD) * n) % MOD;
printf("%d\n", res);

Java implementation

import java.util.*;
 
public class Main
{
  public final static long MOD = 1000000007;
  
  static long PowMod(long x, long n, long m)
  {
    if (n == 0) return 1;
    if (n % 2 == 0) return PowMod((x * x) % m, n / 2, m);
    return (x * PowMod(x, n - 1, m)) % m;
  }

  public static void main(String[] args)
  {
    Scanner con = new Scanner(System.in);
    long n = con.nextLong();
    long res = (PowMod(n - 1, n - 1, MOD) * n) % MOD;
    System.out.println(res);
    con.close();
  }
}

Python implementation — function myPow

The myPow function computes the value of $x^{n} m o d m$ .

def myPow(x, n, m):
  if (n == 0): return 1
  if (n % 2 == 0): return myPow((x * x) % m, n / 2, m)
  return (x * myPow(x, n - 1, m)) % m

The main part of the program. Specify the modulus $m o d = 1 0^{9} + 7$ to be used for the computations.

mod = 10 ** 9 + 7

Read the input value of $n$ .

n = int(input())

Compute and print the answer.

print(n * myPow(n - 1, n - 1, mod) % mod)

Python implementation

Let's define the modulus $m o d = 1 0^{9} + 7$ for the computations.

mod = 10 ** 9 + 7

Read the input value of $n$ .

n = int(input())

Compute and print the answer.

print(n * pow(n - 1, n - 1, mod) % mod)