Editorial

Let's represent a string of length $n$ as the concatenation of two non-empty palindromes of lengths $l$ and $n - l$ . In a palindrome of length $l$ , the first $(l + 1) /2$ letters can be chosen arbitrarily (any of the $k$ letters available), and the remaining letters should be chosen to form a palindrome. This can be done in $k^{(l + 1) /2}$ ways.

Similarly, in a palindrome of length $n - l$ , the first $(n - l + 1) /2$ letters can be chosen arbitrarily, and the remaining letters should form a palindrome. This can be done in $k^{(n - l + 1) /2}$ ways.

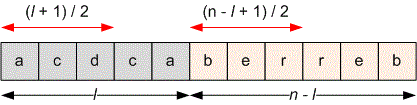
Constructing the concatenation of two palindromes with lengths $l$ and $n - l$ can be done in

k^{(l + 1) /2} \cdot k^{(n - l + 1) /2}

ways. Since neither of the palindromes should be empty, then $1 \leq l \leq n - 1$ . The total number of possible palindromes is

l = 1 \sum n - 1 k^{\frac{( l + 1 )}{2}} \cdot k^{\frac{( n - l + 1 )}{2}}

All operations should be carried out modulo $1 0^{9} + 7$ .

Algorithm realization

The computations are performed modulo $1 0^{9} + 7$ . Let's define the modulo $MO D$ .

#define MOD 1000000007

The powmod function computes the value of $x^{n} m o d m$ .

long long powmod(long long x, long long n, long long m)
{
  if (n == 0) return 1;
  if (n % 2 == 0) return powmod((x * x) % m, n / 2, m);
  return (x * powmod(x, n - 1, m)) % m;
}

The main part of the program. Read the input data.

scanf("%d %d", &n, &k);

Compute the answer $res$ using the formula.

res = 0;
for (l = 1; l < n; l++)
  res = (res + powmod(k, (l + 1) / 2, MOD) * 
               powmod(k, (n - l + 1) / 2, MOD)) % MOD;

Print the answer.

printf("%lld\n", res);

Java realization

import java.util.*;
 
public class Main
{
  public final static long MOD = 1000000007;
  
  static long PowMod(long x, long n, long m)
  {
    if (n == 0) return 1;
    if (n % 2 == 0) return PowMod((x * x) % m, n / 2, m);
    return (x * PowMod(x, n - 1, m)) % m;
  }

  public static void main(String[] args)
  {
    Scanner con = new Scanner(System.in);
    long n = con.nextLong();
    long k = con.nextLong();    
    long res = 0;
    for (long l = 1; l < n; l++)
      res = (res + PowMod(k, (l + 1) / 2, MOD) * 
                   PowMod(k, (n - l + 1) / 2, MOD)) % MOD;
    System.out.println(res);
    con.close();
  }
}

Python realization

The computations are performed modulo $1 0^{9} + 7$ . Let's define the modulo $m o d$ .

mod = 10 ** 9 + 7

Read the input data.

n, k = map(int, input().split())

Compute the answer $res$ using the formula.

res = 0;
for l in range(1,n):
  res = (res + pow(k, (l + 1) // 2, mod) * 
               pow(k, (n - l + 1) // 2, mod)) % mod;

Print the answer.

print(res)