Editorial

The number $a_1$ can range from $1$ to $n$. Given a fixed value of $a_1$, the remaining numbers in the sequence $a_2,...,a_n$ are uniquely determined. Iterate $a_1$ from $1$ to $n$, restore the sequence $a$ and verify whether it constitutes a permutation of numbers from $1$ to $n$ (all $a_i$ must be distinct and fall within the range from $1$ to $n$). Once the reconstructed sequence $a$ forms a permutation, print it and terminate the program.

Since $b_i=a_i+a_{i+1}$, then $a_{i+1}=b_i-a_i$ or $a_i=b_{i-1}-a_{i-1}$.

Example

Let $a_1=3$. Then sequence $b=(4,6,7,6)$ generates the following sequence $a$:

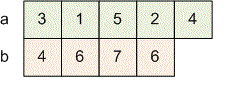
The sequence $a=(3,1,5,2,4)$ is a permutation. The following relationship holds: $3+1=4,1+5=6,5+2=7$ and $2+4=6$.

If, for example, we choose $a_1=1$, then the following sequence $a$ will be restored from the input sequence $b=(4,6,7,6)$:

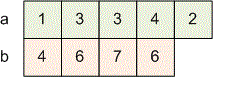
The sequence $a=(1,3,3,4,2)$ is not a permutation.

Algorithm realization

Declare the arrays. The array $used$ will be used to verify whether $a$ is a permutation.

#define MAX 1001
int a[MAX], b[MAX], used[MAX];

Read the input data.

scanf("%d", &n);
for (i = 0; i < n - 1; i++)
  scanf("%d", &b[i]);

Iterate over the value of $a_0$ from $1$ to $n$.

for (a0 = 1; a0 <= n; a0++)
{
  a[0] = a0;

Compute the elements of the sequence $a$ using the formula $a_i=b_{i-1}-a_{i-1}$.

  for (i = 1; i < n; i++)
    a[i] = b[i - 1] - a[i - 1];

Initialize the array $used$ with zeroes.

  for (i = 1; i <= n; i++) used[i] = 0;

Check if $a$ is a permutation. Each value of $a_i$ must appear in the sequence only once and be within the range from $1$ to $n$. The variable $flag$ will be set to $1$ if the sequence $a$ is not a permutation.

  flag = 0;
  for (i = 0; i < n; i++)
  {
    if (a[i] < 1 || a[i] > n || used[a[i]])
    {
      flag = 1;
      break;
    }
    used[a[i]] = 1;
  }

If the sequence $a$ is a permutation, print it and terminate the program.

  if (flag == 0)
  {
    for (i = 0; i < n; i++)
      printf("%d ", a[i]);
    printf("\n");
    return 0;
  }
}

Python realization

Read the input data.

n = int(input())
b = list(map(int, input().split()))

Declare the lists. The list $used$ will be used to check if $a$ is a permutation.

a = [0] * n
used = [0] * (n + 1)

Iterate over the value of $a_0$ from $1$ to $n$.

for a0 in range(1, n + 1):
  a[0] = a0

Compute the elements of the sequence $a$ using the formula $a_i=b_{i-1}-a_{i-1}$.

  for i in range(1, n):
    a[i] = b[i - 1] - a[i - 1]

Initialize the list $used$ with zeroes.

  for i in range(1, n + 1):
    used[i] = 0

Check if $a$ is a permutation. Each value of $a_i$ must appear in the sequence only once and be within the range from $1$ to $n$. The variable $flag$ will be set to $1$ if the sequence $a$ is not a permutation.

  flag = 0
  for i in range(n):
    if a[i] < 1 or a[i] > n or used[a[i]]:
      flag = 1
      break
    used[a[i]] = 1

If the sequence $a$ is a permutation, print it and terminate the program.

  if flag == 0:
    print(*a)
    break