Editorial
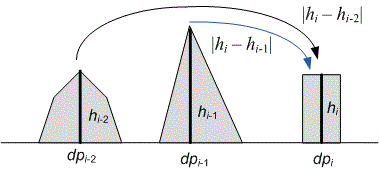
Let be the minimum cost of moving the frog to stone . Then:
(no need to move anywhere),
;
The frog can jump to the -th stone:
either from the -th stone with a cost of ;
or from the -th stone with a cost of ;
Hence
Example
For the given example, the frog’s path with a cost of looks like:
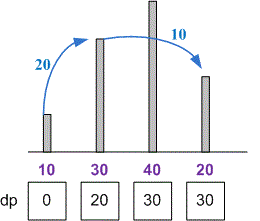
;
;
;
;
Exercise
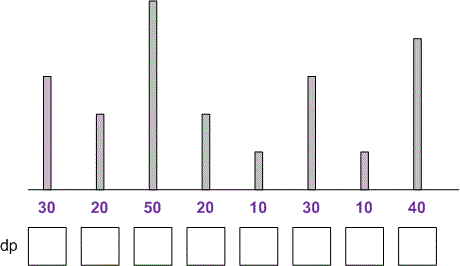
Fill the array for the following example:
Algorithm realization
Declare the arrays.
#define MAX 100001 int h[MAX], dp[MAX];
Read the input data. Store the heights of the stones in the array .
scanf("%d", &n);
for (i = 1; i <= n; i++)
scanf("%d", &h[i]);Initialize the values of and .
dp[1] = 0; dp[2] = abs(h[2] - h[1]);
Compute the values of .
for (i = 3; i <= n; i++)
{
a = dp[i - 1] + abs(h[i] - h[i - 1]);
b = dp[i - 2] + abs(h[i] - h[i - 2]);
dp[i] = min(a, b);
}Print the answer.
printf("%d\n", dp[n]);Java realization
import java.util.*;
class Main
{
static int h[], dp[];
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
h = new int[n+1];
dp = new int[n+1];
for(int i = 1; i <= n; i++)
h[i] = con.nextInt();
dp[1] = 0; dp[2] = Math.abs(h[2] - h[1]);
for (int i = 3; i <= n; i++)
{
int a = dp[i - 1] + Math.abs(h[i] - h[i - 1]);
int b = dp[i - 2] + Math.abs(h[i] - h[i - 2]);
dp[i] = Math.min(a, b);
}
System.out.println(dp[n]);
con.close();
}
}Python realization
Read the input data. Store the heights of the stones in the list .
n = int(input()) h = list(map(int, input().split()))
Initialize the list and assign values to and .
dp = [0] * (n + 1) dp[1] = 0 dp[2] = abs(h[1] - h[0])
Compute the values of .
for i in range(3, n + 1): a = dp[i - 1] + abs(h[i - 1] - h[i - 2]) b = dp[i - 2] + abs(h[i - 1] - h[i - 3]) dp[i] = min(a, b)
Print the answer.
print(dp[n])