Editorial

Let $v$ be a vertex of the tree. Let's define:

$d p_{1} (v)$ as the maximum sum of coins that can be collected from the subtree rooted at $v$ if we take the coins in vertex $v$ .
$d p_{2} (v)$ as the maximum sum of coins that can be collected from the subtree rooted at $v$ if we do not take the coins in vertex $v$ .

Then the answer to the problem will be $ma x (d p_{1} (1), d p_{2} (1))$ , assuming the first vertex is taken as the root of the tree.

Let’s define the given functions recursively:

If we take the coins in vertex $v$ , then we cannot take coins from its children:

d p_{1} (v) = c_{v} + i = 1 \sum k d p_{2} (t o_{i}), w h ere t o_{1}, ..., t o_{k} a re t h e so n s o f v er t e x v .

If we do not take the coins in vertex $v$ , then we can choose either to take or not take coins from its children. We select the option with the maximum sum of coins:

d p_{2} (v) = i = 1 \sum k ma x (d p_{1} (t o_{i}), d p_{2} (t o_{i})), w h ere t o_{1}, ..., t o_{k} a re t h e so n s o f v er t e x v .

If $v$ is a leaf with $c_{v}$ coins, then the functions take the following values: $d p_{1} (v) = c_{v}$ and $d p_{2} (v) = 0$ .

Example

Let's assign the labels $d p_{1} (v) / d p_{2} (v)$ to the vertices of the trees from the examples.

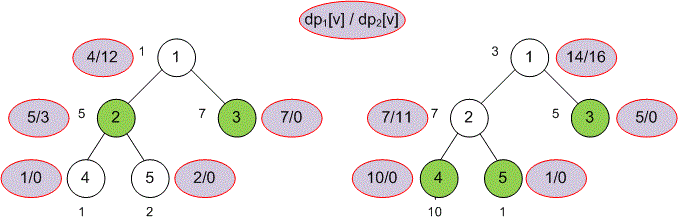
For the first example, we have:

$d p_{1} (1) = c_{1} + d p_{2} (2) + d p_{2} (3) = 1 + 3 + 0 = 4$ ;
$d p_{2} (1) = ma x (d p_{1} (2), d p_{2} (2)) + ma x (d p_{1} (3), d p_{2} (3)) = 5 + 7 = 12$ ;
$d p_{1} (2) = c_{2} + d p_{2} (4) + d p_{2} (5) = 5 + 0 + 0 = 5$ ;
$d p_{2} (2) = ma x (d p_{1} (4), d p_{2} (4)) + ma x (d p_{1} (5), d p_{2} (5)) = 1 + 2 = 3$ ;

For the second example, we have:

$d p 1 (1) = c_{1} + d p_{2} (2) + d p_{2} (3) = 3 + 11 + 0 = 14$ ;
$d p_{2} (1) = ma x (d p_{1} (2), d p_{2} (2)) + ma x (d p_{1} (3), d p_{2} (3)) = 11 + 5 = 16$ ;
$d p_{1} (2) = c_{2} + d p_{2} (4) + d p_{2} (5) = 7 + 0 + 0 = 7$ ;
$d p_{2} (2) = ma x (d p_{1} (4), d p_{2} (4)) + ma x (d p_{1} (5), d p_{2} (5)) = 10 + 1 = 11$ ;

Exercise

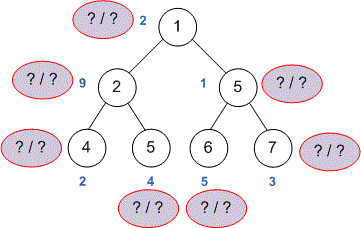
Assign the labels $d p_{1} (v) / d p_{2} (v)$ to the vertices of the tree:

Algorithm realization

Declare the arrays.

vector<vector<int> > g;
vector<int> dp1, dp2, cost;

The dfs function implements depth-first search. Compute the values of $d p_{1}$ and $d p_{2}$ at all vertices of the tree.

void dfs(int v, int p = -1)
{
  dp1[v] = cost[v];
  dp2[v] = 0;

  for (int to : g[v])
  {
    if (to == p) continue;

    dfs(to, v);

    dp1[v] += dp2[to];
    dp2[v] += max(dp1[to], dp2[to]);
  }
}

The main part of the program. Read the tree and the array of coins.

scanf("%d",&n);
g.resize(n+1);
for(i = 1; i < n; i++)
{
  scanf("%d %d",&u,&v);
  g[u].push_back(v);
  g[v].push_back(u);
}

dp1.resize(n+1); dp2.resize(n+1);
cost.resize(n+1);
for(i = 1; i <= n; i++)
  scanf("%d",&cost[i]);

Let the root of the tree be at vertex $1$ . Start the depth-first search from there.

dfs(1);

Compute and print the answer.

ans = max(dp1[1], dp2[1]);
printf("%d\n",ans);