Editorial

In this problem you must construct a matrix of the shortest paths between all pairs of vertices in a graph. To do this, the Floyd-Warshall algorithm should be implemented.

Example

The graph described in the problem statement is as follows:

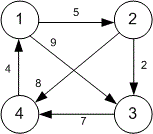
Algorithm realization

Store the adjacency matrix of the graph in the array $g$ .

#define MAX 101
int g[MAX][MAX];

The floyd function implements the Floyd — Warshall algorithm.

void floyd(void)
{
  int i, j, k;
  for(k = 0; k < n; k++)
  for(i = 0; i < n; i++)
  for(j = 0; j < n; j++)
    if (g[i][k] + g[k][j] < g[i][j]) g[i][j] = g[i][k] + g[k][j];
}

The main part of the program. Read the input graph.

scanf("%d",&n);
for(i = 0; i <  n; i++)
for(j = 0; j <  n; j++)
  scanf("%d",&g[i][j]);

Run the Floyd — Warshall algorithm.

floyd();

Print the matrix of the shortest distances between all pairs of vertices.

for(i = 0; i <  n; i++)
{
  for(j = 0; j <  n; j++)
    printf("%d ",g[i][j]);
  printf("\n");
}

Java realization

import java.util.*;

public class Main 
{
  static int g[][];
  static int n;
  
  static void floyd()
  {
    for(int k = 0; k < n; k++)
    for(int i = 0; i < n; i++)
    for(int j = 0; j < n; j++)
      if (g[i][k] + g[k][j] < g[i][j]) 
        g[i][j] = g[i][k] + g[k][j];
  }
  
  public static void main(String[] args) 
  {
    Scanner con = new Scanner(System.in);	  
    n = con.nextInt();
    g = new int[n][n];

    for(int i = 0; i < n; i++)
    for(int j = 0; j < n; j++)
      g[i][j] = con.nextInt();

    floyd();

    for (int i = 0; i < n; i++)
    {
      for (int j = 0; j < n; j++)
    	  System.out.print(g[i][j] + " ");
      System.out.println();
    }
    con.close();
  }
}

Python realization

The floyd function implements the Floyd — Warshall algorithm.

def floyd():
  for k in range(n):
    for i in range(n):
      for j in range(n):
        if g[i][k] + g[k][j] < g[i][j]:
           g[i][j] = g[i][k] + g[k][j]

The main part of the program. Read the input graph.

n = int(input())
g = [[] for _ in range(n)]
for i in range(n):
  g[i] = list(map(int, input().split()))

Run the Floyd — Warshall algorithm.

floyd()

Print the matrix of the shortest distances between all pairs of vertices.

for i in range(n):
  print(*g[i])