Editorial
Let be the adjacency matrix of the graph. Since the graph is undirected, if there is an edge between vertices and , the following equality holds:
The number of edges in the graph equals the number of ones in the adjacency matrix divided by .
Example
The graph given in the example, has the form:
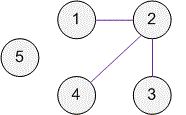
The number of roads on the planet is .
Algorithm realization
Read the input value of .
scanf("%d",&n);Read the adjacency matrix. Compute the sum of the numbers in it. Since the graph is undirected, is equal to twice the number of edges.
res = 0;
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
{
scanf("%d",&val);
res += val;
}Compute and print the number of edges.
res /= 2;
printf("%d\n",res);Java realization
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int res = 0;
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
res += con.nextInt();
res /= 2;
System.out.println(res);
con.close();
}
}Python realization — on fly
Read the input value of .
n = int(input())
The sum of the numbers in the adjacency matrix is stored in the variable .
res = 0
Read the adjacency matrix row by row. For each row, compute the sum of the numbers in it. Then add this sum to .
for _ in range(n): res += sum(map(int, input().split()))
Since the graph is undirected, the sum is equal to twice the number of edges. Divide by and print the answer.
res //= 2 print(res)
Python realization — adjacency matrix
Read the input data.
n = int(input()) g = [[int(j) for j in input().split()] for i in range(n)]
Compute the sum of the numbers in the adjacency matrix. Since the graph is undirected, this sum is equal to twice the number of edges.
s = 0 for row in g: s += sum(row)
Print the number of edges.
print(s // 2)