Сортировка дисков

Имеется $n+1$ стержней и $3n$ дисков. Изначально каждый из первых $n$ стержней содержит ровно $3$ диска. Каждый диск имеет один из $n$ цветов, обозначенных номерами от $1$ до $n$. При этом имеется ровно $3$ диска каждого из $n$ цветов. Стержень номер $n+1$ пуст.

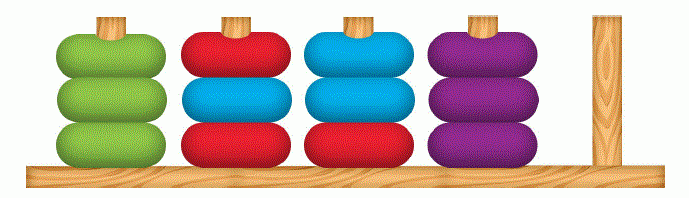
На каждом шаге мы можем выбрать два стержня $a$ и $b(a\ne b)$ так, чтобы $a$ имел как минимум $1$ диск и $b$ имел не более $2$ диска, и переместить верхний диск со стержня $a$ на вершину стержня $b$. Обратите внимание, что ни один стержень не может содержать более $3$ дисков одновременно.

Ваша цель — отсортировать диски. В частности, вы должны выполнить ряд операций (потенциально $0$), чтобы в конце каждый из первых $n$ стержней содержал ровно $3$ диска одного цвета, а $(n+1)$-ый стержень был пустым.

Найдите решение для сортировки дисков максимум за $6n$ операций. Можно доказать, что при этом условии решение всегда существует. Если существует несколько решений, выведите любое.

Входные данные

Первая строка содержит натуральное число $n(1\le n\le 1000)$. Каждая из следующих $3$ строк содержит $n$ натуральных чисел $c_{i,j}(1\le i\le 3,1\le j\le n,1\le c_{i,j}\le n)$ — цвет каждого диска, изначально размещенного на стержнях. Первая из $3$ строк указывает на верхний ряд дисков, вторая строка указывает на средний ряд, а третья строка указывает на нижний ряд.

Выходные данные

Первая строка должна содержать неотрицательное целое число $k(0\le k\le 6n)$ — количество операций. Каждая из следующих $k$ строк должна содержать два различных числа $a_i,b_i(1\le a_i,b_i\le n+1$, для всех $1\le i\le k)$, представляющих $i$-ую операцию (как написано в условии).

Примеры