Не такой уж и плоский

Любое положительное целое число v может быть представлено в виде p_1^a1*p_2^a2*...*p_n^an, где p_i — простое число, а a_i ≥ 0. Например: 24 = 2^3*3^1.
Выберите любые два различных простых числа p_1 и p_2. Представьте двумерную плоскость, где степени p_1 откладываются по оси x, а степени p_2 — по оси y. Теперь любое число, которое может быть записано как p_1^a1*p_2^a2, можно изобразить на этой плоскости в точке (x, y) = (a_1, a_2). На рисунке справа показаны несколько примеров, где p_1 = 3 и p_2 = 2.
Эту идею можно расширить на любое N-мерное пространство, где каждой из N осей присваивается уникальное простое число. Каждое N-мерное пространство имеет уникальный набор простых чисел. Мы называем такой набор Набором Идентификации Пространства или сокращенно S. |S| (порядок S) равен N.
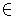
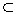
Любое число, которое может быть выражено как произведение p_iS (каждое возведено в степень (a_i ≥ 0), может быть нанесено в этом |S|-мерном пространстве. Рисунок внизу иллюстрирует эту идею для N = 3 и S = {2, 3, 7}. Очевидно, что любое число, которое может быть нанесено на пространство A, также может быть нанесено на пространство B, если S_A ⊆ S_B.
Мы определяем расстояние между любыми двумя точками в заданном N-мерном пространстве как сумму единиц, пройденных для перехода от одной точки к другой, следуя линиям сетки (т.е. движение всегда параллельно одной из осей). Например, на рисунке ниже расстояние между 168 и 882 равно 4.
Даны два положительных целых числа, напишите программу, которая определяет минимальный порядок пространства, в котором оба числа могут быть нанесены. Программа также определяет расстояние между этими двумя числами в этом пространстве.

Входные данные
Ваша программа будет тестироваться на одном или нескольких тестовых случаях. Каждый тестовый случай задан в строке с двумя положительными целыми числами (0 < A, B < 1, 000, 000), где A*B > 1.
Последняя строка состоит из двух нулей.
Выходные данные
Для каждого тестового случая выведите следующую строку:
k. X:D
Где k — номер тестового случая (начиная с единицы), X — минимальный порядок, необходимый в пространстве, в котором могут быть нанесены оба числа A и B. D — расстояние между этими двумя точками.
Примечание: Перед X стоит пробел.