Разбор

В ориентированном графе следует найти количество сильно связных компонент.

Пример

Графы, приведенные в примерах, имеют вид:

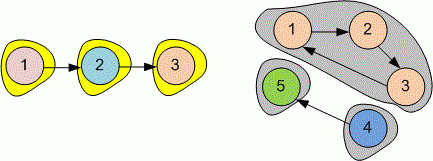
Каждый из графов содержит $3$ сильно связные компоненты.

Реализация алгоритма

Входной граф храним в списке смежности $g$ . Обратный граф храним в $g r$ .

vector<vector<int> > g, gr;
vector<int> used, top;

Функция dfs1 реализует поиск в глубину на входном графе. В массив $t o p$ заносим последовательность вершин, в которой поиск в глубину завершает их обработку.

void dfs1(int v)
{
  used[v] = 1;
  for (int to : g[v])
    if (!used[to]) dfs1(to);
  top.push_back(v);
}

Функция dfs2 реализует поиск в глубину на обратном графе. Все вершины, которые будут пройдены в результате рекурсивного вызова функции dfs2, принадлежат одной компоненте сильной связности.

void dfs2(int v)
{
  used[v] = 1;
  for (int to : gr[v])
    if (!used[to]) dfs2(to);
}

Основная часть программы. Читаем входные данные. Строим обратный граф.

scanf("%d %d", &n, &m);
g.resize(n + 1);
gr.resize(n + 1);
for(i = 1; i <= m; i++)
{
  scanf("%d %d",&a,&b);
  g[a].push_back(b);
  gr[b].push_back(a);
}

Запускаем поиск в глубину на входном графе. Последовательность, в которой завершается обработка вершин графа, сохраняется в массиве $t o p$ .

used.resize(n+1);
for(i = 1; i <= n; i++)
  if (!used[i]) dfs1(i);

Запускаем поиск в глубину на обратном графе. Вершины обратного графа следует рассматривать в порядке обхода массива $t o p$ справа налево (с конца в начало). Для удобства дальнейшей обработки обернем массив $t o p$ .

used.clear();
used.resize(n + 1);
reverse(top.begin(), top.end());

В переменной $c$ подсчитываем количество сильно связных компонент.

c = 0;

Теперь двигаемся по массиву $t o p$ слева направо и вызываем из каждой еще непосещенной вершины поиск в глубину dfs2.

for (int v : top)
  if (!used[v])
  {
    dfs2(v);
    c++;
  }

Выводим количество компонент сильной связности графа.

printf("%d\n",c);

Java реализация

import java.util.*;

public class Main
{
  static ArrayList<Integer>[] g, gr;	
  static boolean used[];
  static Vector<Integer> top = new Vector<Integer>();

  static void dfs1(int v)
  {
    used[v] = true;
    for(int i = 0; i < g[v].size(); i++)
    {
      int to = g[v].get(i);
      if (!used[to]) dfs1(to);
    }
    top.add(v);
  }

  static void dfs2(int v)
  {
    used[v] = true;
    for(int i = 0; i < gr[v].size(); i++)
    {
      int to = gr[v].get(i);
      if (!used[to]) dfs2(to);
    }
  }
  
  @SuppressWarnings("unchecked")  
  public static void main(String[] args)
  {
    Scanner con = new Scanner(System.in);
    int n = con.nextInt();
    int m = con.nextInt();
    
    g = new ArrayList[n+1];
    for(int i = 0; i <= n; i++)
      g[i] = new ArrayList<Integer>();
    gr = new ArrayList[n+1];
    for(int i = 0; i <= n; i++)
      gr[i] = new ArrayList<Integer>();
    
    for (int i = 0; i < m; i++)
    {
      int a = con.nextInt();
      int b = con.nextInt();
      g[a].add(b);
      gr[b].add(a);
    }

    used = new boolean[n+1];
    for(int i = 1; i <= n; i++)
      if (!used[i]) dfs1(i);
    
    used = new boolean[n+1];
    int c = 0;
    for(int i = 1; i <= n; i++)
    {
      int v = top.get(n-i);
      if (!used[v])
      {
        dfs2(v);
        c++;
      }
    }
    
    System.out.println(c);
    con.close();
  }
}

Python realization

def dfs1(v):
  global g, used, top
  used[v] = True
  for to in g[v]:
    if not used[to]: dfs1(to)
  top.append(v)

def dfs2(v):
  global gr, used
  used[v] = True
  for to in gr[v]:
    if not used[to]: dfs2(to)

Основная часть программы. Читаем входные данные. Строим обратный граф.

n, m = map(int, input().split())
g = [[] for _ in range(n + 1)]
gr = [[] for _ in range(n + 1)]

for _ in range(m):
  a, b = map(int, input().split())
  g[a].append(b)
  gr[b].append(a)

used = [False] * (n + 1)
top = []

for i in range(1, n + 1):
  if not used[i]: dfs1(i)

used = [False] * (n + 1)
top.reverse()

В переменной $c$ подсчитываем количество сильно связных компонент.

c = 0

for v in top:
  if not used[v]:
    dfs2(v)
    c += 1

Выводим количество компонент сильной связности графа.

print(c)