Recursion and Iteration
When we start learning the basics of programming, as a rule, the first program we write prints the string "Hello, world!". Then we get acquainted with variables, operators, functions. And usually, the first ones a beginner gets to know are the conditional operator and the loop operator. Immediately, there is a desire to write some simple function: the factorial of a number, raising to a power, or calculating the binomial coefficient. In most cases, a beginner programmer implements the iterative version of functions. However, few know that any iterative function can also be implemented recursively.
Recursion is a method of data processing organization in which the program (or function) calls itself either directly or from other programs (functions).
A function is called recursive if, during its processing, it is called again, either directly or indirectly, through a chain of calls of other functions.

Iteration is a method of data processing organization in which some actions are repeatedly performed, not leading to recursive calls of programs (functions).
Theorem. Any algorithm implemented in recursive form can be rewritten in iterative form and vice versa.
Next, we will consider a set of elementary functions, implemented both using loop operators and using a recursive approach. Before writing recursive functions in any programming language, it is usually necessary to write a recurrence relation that defines the method of calculating functions. The recurrence relation must contain at least two conditions:
I) the condition for continuing recursion (recursion step);
II) the condition for ending recursion.
Recursion will be implemented using a call to the function itself. In this case, the condition for continuing recursion should be checked first in the body of the function. If it is true, then we exit the function. Otherwise, we make a recursive step.
The iterative version of functions will be implemented using the for loop operator.
1. Factorial of a number. The factorial of a non-negative integer is the product of all natural numbers from 1 to and is denoted by !. If !, then the following recurrence relation holds:
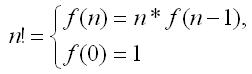
The first equation describes the recursion step – the method of calculating through . The second equation indicates when to stop calculating the function. If it is not set, then the function will work indefinitely.
For example, the value can be calculated as follows:
Obviously, calculating requires making recursive calls.
recursive implementation | cyclic implementation |
|---|---|
|
|
The idea of the cyclic implementation is to directly calculate the factorial of a number using the loop operator:
2. Power of a number in linear time. Calculating the power of a number with a linear (O()) time estimate can be defined using the following recurrence relation:
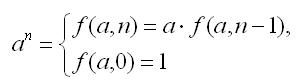
recursive implementation | cyclic implementation |
|---|---|
|
|
In the iterative version, it is enough to calculate the product ( factors of ).
3. Power of a number in logarithmic time. Calculating the power of a number with a time estimate of O(log) is defined as follows:
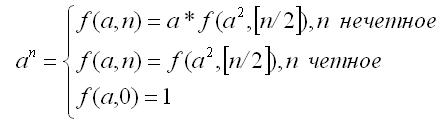
For example, raising to the tenth power can be implemented as follows:
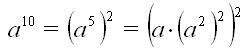
Since squaring is equivalent to one multiplication, to calculate , it is enough to perform 4 multiplications.
recursive implementation | cyclic implementation |
|---|---|
|
|
4. Sum of the digits of a number. The sum of the digits of a natural number can be found using the function , defined as follows:
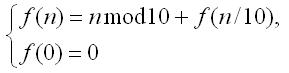
The condition for continuing recursion: the sum of the digits of a number equals the last digit plus the sum of the digits of the number without the last digit (the number divided by 10).
The condition for ending recursion: If the number is 0, then the sum of its digits is 0.
For example, the sum of the digits of the number 234 will be calculated as follows:
recursive implementation | cyclic implementation |
|---|---|
|
|
5. Number of ones. The number of ones in the binary representation of the number can be calculated using the function , defined as follows (& - bitwise 'AND' operation):
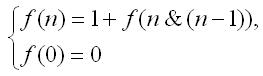
As a result of the operation n = n & (n – 1), the last one in the binary representation of the number is destroyed:
n & (n – 1) = a_1a_2…a_{k-1} 000…0
The recursive call of the function will be made as many times as there are ones in the binary representation of the number .
recursive implementation | cyclic implementation |
|---|---|
|
|
6. Binomial coefficient. The value of the binomial coefficient equals
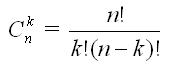
and is defined by the recurrence relation:
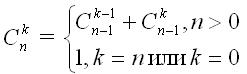
int c(int k, int n){ if (n == k) return 1; if (k == 0) return 1; return c(k - 1, n - 1) + c(k, n - 1);}
Considering that
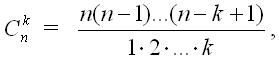
the value of the binomial coefficient can be calculated using a loop. In this case, all division operations will be integer. If , then use the relation
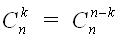
to avoid Time Limit when calculating, for example, the value
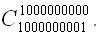
int Cnk(int k, int n){ long long res = 1; if (k > n - k) k = n - k; for (int i = 1; i <= k; i++) res = res * (n - i + 1) / i; return (int)res;}
7. Recursive function. For a given natural , let's calculate the value of the function , defined by the recurrence relations:
The direct implementation of the function looks like this:
int f(int n){ if (n <= 1) return n; if (n % 2) return f(n / 2) + f(n / 2 + 1); return f(n / 2);}
In such an implementation, some values of the function may be calculated several times. Let's consider another approach to calculating the values of . Let's define the function
for which the following equalities hold:
Using the given relations, the value can be calculated with a time estimate of O(log ).
int g(int n, int i, int j){ if (!n) return j; if (n % 2) return g(n / 2, i, i + j); return g(n / 2, i + j, j);}
int f(int n){ return g(n, 1, 0);}
8. Ackermann function. The Ackermann function A(, ) is defined recursively as follows:
A(0, ) = + 1,
A(, 0) = A( – 1, 1),
A(, ) = A( – 1, A(, – 1))
The recursive implementation of the Ackermann function looks like this:
int a(int m, int n){ if (!m) return n + 1; if (!n) return a(m - 1, 1); return a(m - 1, a(m, n - 1));}
For small values of , the Ackermann function can be expressed explicitly:
A(0, ) = + 1
A(1, ) = 2 + ( + 3) – 3 = + 2
A(2, ) = 2 · ( + 3) – 3 = 2 · + 3
A(3, ) = 2 – 3
9. Selection for reconnaissance [ACM, 1999]. From soldiers, lined up in a row, it is necessary to select a few for reconnaissance. To do this, the following operation is performed: if there are more than 3 soldiers in the row, then all soldiers standing in even positions are removed, or all soldiers standing in odd positions are removed. This procedure is repeated until there are 3 or fewer soldiers left in the row. They are sent for reconnaissance. Calculate the number of ways in which such reconnaissance groups can be formed exactly with three people.
Input. The number of soldiers in the row (0 < ≤ 10).
Output. The number of ways in which soldiers can be selected for reconnaissance in the above manner.
Example input | Example output |
|---|---|
|
|
|
|
Solution. Let's denote by the number of ways in which reconnaissance groups can be formed from people in the row. Since we are only interested in groups of three scouts, , , . That is, from three people, only one group can be formed, from one or two – none.
If is even, then by applying the operation defined in the problem for removing soldiers in the row, we will have either / 2 soldiers left, who stood in even positions, or / 2 soldiers, who stood in odd positions. Thus, for even .
If is odd, then after removal, either / 2 soldiers, who stood in even positions, or / 2 + 1 soldier, who stood in odd positions, will remain. The total number of ways for odd equals
Thus, the obtained recurrence formula for calculating the value of :
, if is even
, if is odd
The implementation of the function looks like this:
int f(int n){ if (n <= 2) return 0; if (n == 3) return 1; if (n % 2) return f(n / 2) + f(n / 2 + 1); return 2 * f(n / 2);}
REFERENCES
"Algorithms: Design and Analysis", Cormen T., Leiserson C., Rivest R., Stein C., – Moscow, Saint Petersburg, Kiev, 2005 – 1292 p.
"Practice and Theory of Programming", Book2. "Practice and Theory of Programming", Volume 2. Vinokurov N.A., Vorozhtsov A.V., - Moscow: Fizmatkniga, 2008 - 288 p.