Extended Euclidean Algorithm
The algorithm for computing the greatest common divisor (GCD) was discovered by ancient Greek mathematicians and is known as the "algorithm of mutual subtraction". Although references to this algorithm can be found in Aristotle's works, it was later named after Euclid. What the greatest common divisor is, its properties, and methods of calculation are discussed in [1].
Let's recall that the GCD of two numbers can be calculated according to the following recurrence:
In C language, the procedure for calculating the GCD looks like this:
int gcd(int a, int b)
{
if (b == 0) return a;
return gcd(b, a % b);
}The Euclidean algorithm can be extended to find for given a and b such integers x and y that , where is the greatest common divisor of and .
Lemma. Let for positive integers and () known = GCD(, ) = GCD(, mod ), and also numbers ’ and ’, for which
’ · + ’ · ( mod )
Then the values of and , which are solutions to the equation , are found from the relations
’, ’ – ’ · (2)
Here denotes the integer part of the number a/b.
Proof. Since mod = – · , then
’ · + ’ · ( – · ) = ’ · + (’ – ’ · ) · = · + · ,
where denoted ’, ’ – ’ · .
The function gcdext(int a, int b, int *d, int *x, int *y), shown below, finds = GCD(, ) and such , that for the input numbers and . To find the unknowns and , it is necessary to recursively start the function gcdext(b, a mod b, d, x, y) and recalculate the values of and using the formula above. The recursion ends when . At , GCD(, 0) = and , so we consider , .
void gcdext (int a, int b, int *d, int *x, int *y)
{
int s;
if (b == 0)
{
*d = a; *x = 1; *y = 0;
return;
}
gcdext(b,a % b,d,x,y);
s = *y;
*y = *x - (a / b) * (*y);
*x = s;
}For manual execution of the extended Euclidean algorithm, it is convenient to use a table with four columns (as shown below in the example), corresponding to the values of , , , . The calculation process is divided into three stages:
a) First, we calculate the GCD(, ), using the first two columns of the table and relation (1). In the last row in the column , the value of = GCD(, ) will be found.
b) We enter the values 1 and 0 respectively into the columns and of the last row.
c) We will sequentially fill in the rows for the columns and from bottom to top. The values of and in the last row have already been entered at stage b). Assuming that the values (’, ’) are already located in the current filled row, we will recalculate and enter the values (, ) into the corresponding cells in the row above using formulas (2).
1. Extended Euclidean Algorithm. Find the solution to the equation . The calculation of GCD(5, 3) and finding the corresponding , are done in the table:
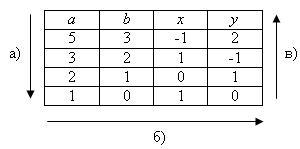
The order and direction of calculations are indicated by arrows and letters.
From the table, we find that GCD(5, 3) = , i.e., , .
Consider, for example, how the values (, ) for the first row were obtained. From the second row, we take the values (’, ’) = (1, -1). According to formulas (2), we get:
’ = -1,
’ – ’ · = 1 – (-1) · = 1 + 1 = 2
Linear Equation is an equation in the form (mod ). It has a solution if and only if is divisible by = GCD(, ). If , the equation can be simplified by replacing it with ’’ (mod ’), where ’ = , ’ = , ’ = . After such a transformation, the numbers ’ and ’ are coprime.
The algorithm for solving the equation ’’ (mod ’) with coprime ’ and ’ consists of two parts:
Solve the equation ’ (mod ’). To do this, use the extended Euclidean algorithm to find the solution (, ) to the equation ’’. Taking the modulus ’ for the last equation, we get ’ (mod ’).
Multiply the equation ’ (mod ’) by ’. We get ’(’) = ’ (mod ’), from which the solution to the initial equation ’’ (mod ’) will be ’ (mod ’).
Lemma. If GCD(, ) = 1, then the equation (mod ) is equivalent to (mod ).
Proof. From (mod ), it follows that () · is divisible by . But since and are coprime, is divisible by , i.e., (mod ).
Example. Solve the equation (mod 8).
The value = GCD(18, 8) = 2 is a divisor of 6, so a solution exists. After simplification, we get the equation (mod 4). According to the lemma, this is equivalent to (mod 4). Solving the equation using the extended Euclidean algorithm, we get , . Hence, (mod 4) = 3. Thus, will be a solution to both the equation (mod 4) and (mod 8).
DIOPHANTINE EQUATIONS
Diophantine are equations in the form
,
where is a polynomial with integer coefficients.
In this section, we will consider the algorithm for finding a solution to a linear Diophantine equation with two unknowns in the form (for simplicity, we will omit multiplication signs and write simply ).
Theorem 1. The equation has a solution in integers if and only if is divisible by GCD(, ).
Theorem 2. If the pair (, ) is a solution to the equation , then the entire set of its solutions (, ) is described by the formula:
,
,
where ∈ Z. Obviously, if , then for any integer .
To find a particular solution (, ) to the equation , one should first find the solution (’, ’) to the equation ( – the greatest common divisor of and ) using the extended Euclidean algorithm, and then multiply it by . That is,
’ · ,
’ ·
Example. Find the set of solutions to the equation .
The equation has a solution, since 7 is divisible by GCD(5, 3) = 1.
Find the solution to the equation ’ + ’ = 1 using the extended Euclidean algorithm: (’, ’) = (-1, 2).
Find the solution (, ) to the initial Diophantine equation:
,
According to Theorem 2, the set of solutions to the initial Diophantine equation is:
(, ) = (-7 + 3, 14 – 5)