•Статті•1 рік тому

Біноміальний коефіцієнт

Сполученням з $n$ елементів по $k$ називається набір з $k$ елементів, вибраних із заданих $n$ елементів. При цьому набори, які відрізняються тільки порядком слідування елементів (але не складом), вважаються однаковими. Саме завдяки цій властивості сполучення відрізняються від розміщень.

Наприклад, розглянемо множину з $5$ елементів: ${1, 2, 3, 4, 5}$ . Набори ${2, 1, 3}$ і ${3, 2, 1}$ є однаковими як сполучення (хоча різні як розміщення), оскільки складені з тих самих елементів ${1, 2, 3}$ .

Формула для обчислення кількості сполучень з $n$ по $k$ дорівнює

C_{n}^{k} = \frac{n !}{k ! \cdot ( n - k )!}

Числа $C_{n}^{k}$ називаються біноміальними коефіцієнтами.

Коли ми вибираємо нуль елементів із множини з $n$ елементів, ми фактично робимо “пустий” вибір. Порожня множина, в цьому контексті, вважається допустимим сполученням. Уявіть, що у вас є коробка з $n$ кулями, і ви хочете вибрати $0$ з них. Навіть якщо ви нічого не вибираєте, це все одно є допустимим варіантом вибору. Таким чином, $C_{n}^{0}$ означає кількість способів вибрати $0$ елементів з $n$ , що дорівнює $1$ .

Ми можемо розглядати це як один єдиний спосіб не вибирати жоден елемент з множини, що і дає результат $1$ .

C_{n}^{0} = \frac{n !}{0 ! \cdot ( n - 0 )!} = \frac{n !}{1 ! \cdot n !} = 1

Коли ми вибираємо один елемент із множини з $n$ елементів, у нас є $n$ варіантів вибору: ми можемо вибрати будь-який з $n$ елементів. Наприклад, якщо у нас є множина з чисел від $1$ до $5$ ( ${1, 2, 3, 4, 5}$ ), то ми можемо вибрати одне число з цієї множини, і у нас є $5$ варіантів для цього вибору.

Значення $C_{n}^{1}$ дорівнює $n$ , тому що є $n$ способів вибрати один елемент з множини з $n$ елементів.

C_{n}^{1} = \frac{n !}{1 ! \cdot ( n - 1 )!} = n

При виборі $2$ елементів із $n$ — елементної множини, ми формуємо комбінації пар. Для побудови такої пари ми спочатку вибираємо один елемент, а потім другий.

Перший елемент можна вибрати з $n$ елементів.
Після вибору першого елемента, у нас залишається $n -1$ елемент для вибору другого елемента (оскільки ми не можемо вибрати повторно той самий елемент).

Таким чином, загальна кількість комбінацій пар елементів, які можна вибрати з $n$ — елементної множини, дорівнює добутку числа способів вибрати перший і другий елементи: $n \cdot (n -1)$ .

Проте, кожна пара врахована двічі, оскільки порядок елементів у парі не має значення. Наприклад, $(p, q)$ і $(q, p)$ вважаються однією і тією ж парою. Щоб врахувати це, слід поділити загальну кількість комбінацій на $2$ . Таким чином, $C_{n}^{2}$ дорівнює $n \cdot (n -1) /2$ .

C_{n}^{2} = \frac{n !}{2 ! \cdot ( n - 2 )!} = \frac{n \cdot ( n - 1 )}{2}

Властивість симетрії: $C_{n}^{k} = C_{n}^{n - k}$ .

Кількість способів вибрати $k$ елементів з $n$ дорівнює кількості способів не вибрати $(n - k)$ елементів з $n$ . Але не вибрати $(n - k)$ елементів з $n$ ми можемо $C_{n}^{n - k}$ способами. Відповідно $C_{n}^{k} = C_{n}^{n - k}$ .

Вправа. Обчислити значення наступних біноміальних коефіцієнтів:

1) $C_{5}^{2}$	3) $C_{5}^{4}$	5) $C_{8}^{1}$
2) $C_{8}^{3}$	4) $C_{7}^{5}$	6) $C_{8}^{5}$

Формула додавання: $C_{n}^{k} = C_{n - 1}^{k - 1} + C_{n - 1}^{k}$ .

Доказ. Обчислимо значення правої частини рівняння:

C_{n - 1}^{k - 1} + C_{n - 1}^{k} = \frac{( n - 1 )!}{( k - 1 )! \cdot ( n - k )!} + \frac{( n - 1 )!}{k ! \cdot ( n - k - 1 )!} =

\frac{( n - 1 )! \cdot k + ( n - 1 )! \cdot ( n - k )}{k ! \cdot ( n - k )!} = \frac{( n - 1 )! \cdot ( k + n - k )}{k ! \cdot ( n - k )!} = \frac{n !}{k ! \cdot ( n - k )!} = C_{n}^{k}

Готуючись до іспиту з математичного аналізу, Петя розклав перед собою $n$ різних шпаргалок. Вони були його порятунком, адже за весь семестр Петя так жодного разу не спромігся вивчити матеріал як слід. Шпаргалок виявилося настільки багато, що вони не вміщалися в жодну кишеню. Тому Петя вирішив підрахувати максимальну кількість шпаргалок, яку він зможе взяти з собою на іспит. І тут виникло питання: а скільки взагалі існує способів вибрати потрібну кількість шпаргалок?

Вхідні дані. Містять загальну кількість шпаргалок $n (1 \leq n \leq 12)$ і кількість шпаргалок $k (0 \leq k \leq n)$ , яку Петя може взяти з собою.

Вихідні дані. Виведіть кількість способів вибрати $k$ шпаргалок з $n$ .

Відкрити задачу

Для обчислення біноміального коефіцієнта можна скористатися наступним співвідношенням:

C_{n}^{k} = \frac{n !}{k ! \cdot ( n - k )!} = \frac{n \cdot ( n - 1 ) \cdot ( n - 2 ) \cdot ... \cdot ( n - k + 1 )}{1 \cdot 2 \cdot 3 \cdot ... \cdot k}

Оголосимо змінну $res$ і ініціалізуємо її значенням $1$ . Потім помножимо $res$ на $n$ і розділимо результат на $1$ . Після цього помножимо $res$ на $n -1$ і розділимо на $2$ . Процес множень і ділення будемо продовжувати $k$ разів (чисельник і знаменник $C_{n}^{k}$ після скорочення на $(n - k)!$ містить $k$ множників).

Біноміальні коефіцієнти з'являються в біномі Ньютона:

(x + y)^{n} = k = 0 \sum n C_{n}^{k} x^{k} y^{n - k}

Розглянемо приклади:

(x + y)^{2} = C_{2}^{0} x^{2} y^{0} + C_{2}^{1} x^{1} y^{1} + C_{2}^{2} x^{0} y^{2} = x^{2} + 2 x y + y^{2},

(x + y)^{3} = C_{3}^{0} x^{3} y^{0} + C_{3}^{1} x^{2} y^{1} + C_{3}^{2} x^{1} y^{2} + C_{3}^{3} x^{0} y^{3} = x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3}

Розглянемо $2 n$ об'єктів $a_{1}, ..., a_{2 n}$ і знайдемо кількість способів вибрати $n$ об'єктів з $2 n$ .

Розіб'ємо множину на дві частини: ${a_{1}, a_{2}, ..., a_{n}, a_{n + 1}, ..., a_{2 n}}$ . Щоб вибрати $n$ об'єктів з $2 n$ , нам потрібно вибрати $k (k \leq n)$ об'єктів з лівої половини (тобто з множини ${a_{1}, a_{2}, ..., a_{n}})$ і $n - k$ об'єктів з правої (з множини ${a_{n + 1}, a_{n + 2}, ..., a_{2 n}})$ . Кількість способів зробити такий вибір відповідно до правила множення дорівнює $C_{n}^{k} \cdot C_{n}^{n - k} = (C_{n}^{k})^{2}$ . Оскільки $k$ може приймати значення від $0$ до $n$ , то $\sum_{k = 0}^{n} (C_{n}^{k})^{2}$ дорівнює кількості способів вибрати $n$ об'єктів з $2 n$ , тобто $C_{2 n}^{n}$ . Таким чином

(C_{n}^{0})^{2} + (C_{n}^{1})^{2} + (C_{n}^{2})^{2} + ... + (C_{n}^{n})^{2} = C_{2 n}^{n}

Приклад

Для $n = 3$ відповідь дорівнює $(C_{3}^{0})^{2} + (C_{3}^{1})^{2} + (C_{3}^{2})^{2} + (C_{3}^{3})^{2} = 1^{2} + 3^{2} + 3^{2} + 1^{2} = 20$

Водночас $C_{6}^{3} = \frac{6 !}{3 ! \cdot 3 !} = \frac{4 \cdot 5 \cdot 6}{6} = 20$ .

Розглянемо послідовність із $n$ одиниць: $111...11$ . Між будь-якими двома одиницями можна вставити знак ‘ $+$ ’. Наприклад $11 + 111 + 1$ . Такий запис буде позначати суму $2 + 3 + 1$ , де кожен доданок – кількість одиниць, що стоять поряд. Кількість позицій, куди можна вставити знак ‘ $+$ ’, дорівнює $n -1$ . Оскільки необхідно отримати суму з $k$ доданків, то слід вставити $k -1$ знак ‘ $+$ ’.

Нам слід вставити $k -1$ плюс на $n -1$ місце. Це можна зробити $C_{n - 1}^{k - 1}$ способами.

Приклад

Розглянемо рівняння $x_{1} + x_{2} + x_{3} = 4$ . Воно має $3$ позитивних цілих розв'язки:

$(1, 1, 2)$
$(1, 2, 1)$
$(2, 1, 1)$

Наприклад, $n = 4$ одиниці на $k = 3$ доданків можна розбити $C_{2}^{3} = 3$ способами:

Розглянемо послідовність із $n + k -1$ позицій. У $n$ позиціях слід поставити $1$ . У $k -1$ позицію слід поставити символ ' $+$ ' (щоб отримати $k$ доданків).

Будь-якому розташуванню одиниць і знаків ' $+$ ' по позиціях буде відповідати деякий розв'язок заданого рівняння. Наприклад, розглянемо деякі розв'язки рівняння $x_{1} + x_{2} + x_{3} = 4 (4$ одиниці і $2$ плюси):

Нам слід вставити $k -1$ плюс на $n + k -1$ позицій. Це можна зробити $C_{n + k - 1}^{k - 1}$ способами.

Приклад

Розглянемо рівняння $x_{1} + x_{2} + x_{3} = 4$ . Його розв'язками будуть:

$(4, 0, 0)$ і її $3$ перестановки
$(3, 1, 0)$ і її $6$ перестановок
$(2, 2, 0)$ і її $3$ перестановки
$(2, 1, 1)$ і її $3$ перестановки

Усього є $3 + 6 + 3 + 3 = 15$ розв'язків.

Обчислення будемо проводити з використанням $64$ -розрядних беззнакових цілих чисел (unsigned long long). Очевидно, що

C_{n}^{k} = \frac{n !}{k ! \cdot ( n - k )!} = \frac{n \cdot ( n - 1 ) \cdot ( n - 2 ) \cdot ... \cdot ( n - k + 1 )}{1 \cdot 2 \cdot 3 \cdot ... \cdot k} = \frac{n}{1} \cdot \frac{n - 1}{2} \cdot \frac{n - 2}{3} \cdot ... \cdot \frac{n - k + 1}{k}

Присвоїмо змінній $res$ значення $1$ , після чого будемо її множити на $\frac{n - i + 1}{i}$ для всіх $i$ від $1$ до $k$ . Кожного разу ділення на $i$ буде цілочисельним, проте при множенні можна отримати переповнення. Нехай $d = НОД (res, i)$ . Тоді операцію

res = res * (n - i + 1) / i

перепишемо через

res = (res / d) * ((n - i + 1) / (i / d))

При такій реалізації переповнення при множенні не відбудеться (відповідь є $64$ -розрядним беззнаковим цілим числом). Зазначимо, що спочатку слід виконати ділення $(n - i + 1) / (i / d)$ , а потім множення $res / d$ на отримане частке.

Для обчислення $C_{n}^{k}$ слід виконати $k$ ітерацій. Але що робити, якщо слід обчислити $C_{2000000000}^{1999999999}$ ? Відповідь не перевищить $2^{64}$ , тому такі вхідні дані можливі. Оскільки $C_{n}^{k} = C_{n}^{n - k}$ , то при $n - k < k$ слід покласти $k = n - k$ .

Приклад

Розглянемо наступний приклад:

C_{6}^{3} = \frac{6}{1} \cdot \frac{5}{2} \cdot \frac{4}{3} = 15 \cdot \frac{4}{3}

Нехай $res = 15$ , і залишилось виконати множення $res \cdot \frac{4}{3} = 15 * \frac{4}{3}$ . Обчислимо $d = НОД (15, 3) = 3$ . Тому $15 \cdot \frac{4}{3} = (15/3) \cdot \frac{4}{3/3} = 5 \cdot \frac{4}{1} = 20$ .

Функція gcd обчислює найбільший спільний дільник чисел $a$ і $b$ .

unsigned long long gcd(unsigned long long a, unsigned long long b)
{
  return (!b) ? a : gcd(b,a % b);
}

Функція Cnk обчислює значення біноміального коефіцієнта $C_{n}^{k}$ .

unsigned long long Cnk(unsigned long long n, unsigned long long k)
{
  unsigned long long CnkRes = 1, t, i;
  if (k > n - k) k = n - k;
  for(i = 1; i <= k; i++)
  {
    t = gcd(CnkRes, i);
    CnkRes = (CnkRes / t) * ((n - i + 1) / (i / t));
  }
  return CnkRes;
}

Основна частина програми. Читаємо вхідні дані. Послідовно обробляємо тести.

scanf("%d",&t);
while(t--)
{
  scanf("%llu %llu",&n,&k);
  res = Cnk(n,k);
  printf("%llu\n",res);
}

Перепишемо задану суму у вигляді:

1 \cdot C_{n}^{0} + 2 \cdot C_{n}^{1} + 3 \cdot C_{n}^{2} + ... + (n + 1) \cdot C_{n}^{n} =

(C_{n}^{0} + C_{n}^{1} + C_{n}^{2} + ... + C_{n}^{n}) + 1 \cdot C_{n}^{1} + 2 \cdot C_{n}^{2} + ... + n \cdot C_{n}^{n}

Сума у дужках дорівнює $2^{n}$ . Якщо у формулі бінома Ньютона

(a + b)^{n} = i = 0 \sum n C_{n}^{i} a^{i} b^{n - i}

покласти $a = b = 1$ , то отримаємо співвідношення: $(1 + 1)^{n} = \sum_{i = 0}^{n} C_{n}^{i} 1^{i} 1^{n - i}$ , або

2^{n} = i = 0 \sum n C_{n}^{i} = C_{n}^{0} + C_{n}^{1} + ... + C_{n}^{n}

Обчислимо залишок суми:

1 \cdot C_{n}^{1} + 2 \cdot C_{n}^{2} + ... + n \cdot C_{n}^{n} =

1 \cdot \frac{n !}{1 ! \cdot ( n - 1 )!} + 2 \cdot \frac{n !}{2 ! \cdot ( n - 2 )!} + ... + n \cdot \frac{n !}{n ! \cdot ( n - n )!} =

n \cd от (\frac{( n - 1 )!}{0 ! \cdot ( n - 1 )!} + \frac{( n - 1 )!}{1 ! \cdot ( n - 2 )!} + ... + \frac{( n - 1 )!}{( n - 1 )! \cdot ( n - n )!}) =

n \cdot (C_{n - 1}^{0} + C_{n - 1}^{1} + ... + C_{n - 1}^{n - 1}) = n \cdot 2^{n - 1}

Таким чином, відповідь дорівнює $2^{n} + n \cdot 2^{n - 1} = (n + 2) \cdot 2^{n - 1}$ .

Приклад

Обчислимо відповідь для $n = 3$ . При безпосередньому обчисленні:

1 \cdot C_{3}^{0} + 2 \cdot C_{3}^{1} + 3 \cdot C_{3}^{2} + 4 \cdot C_{3}^{3} = 1 \cdot 1 + 2 \cdot 3 + 3 \cdot 3 + 4 \cdot 1 = 1 + 6 + 9 + 4 = 20

При обчисленні за формулою: $5 \cdot 2^{2} = 20$ .

Читаємо вхідне значення $n$ .

scanf("%lld", &n);

Обчислюємо і виводимо відповідь.

res = (1LL << (n - 1)) * (n + 2);
printf("%lld\n", res);

Реалізація алгоритму – функція

Оголосимо масив для запам'ятовування результатів: $d p [n] [k] = C_{n}^{k}$ .

int dp[31][31];

Функція Cnk обчислює значення біноміального коефіцієнта $C_{n}^{k}$ .

int Cnk(int n, int k)
{
  if (n == k) return 1;
  if (k == 0) return 1;
  if (dp[n][k] != -1) return dp[n][k];
  return dp[n][k] = (Cnk(n - 1, k - 1) + Cnk(n - 1, k)) % 9929;
}

Основна частина програми. Читаємо вхідне значення $n$ .

scanf("%d", &n);
memset(dp, -1, sizeof(dp));

Обчислюємо зазначену суму.

res = 0;
for (i = 0; i <= n; i++)
  res += (i + 1) * Cnk(n, i);

Виводимо відповідь.

printf("%d\n", res);

У вас є аркуш паперу, і ви обираєте на ньому прямокутник розміром $n \cdot m$ . Назвемо цей прямокутник разом з лініями, на яких він знаходиться, сіткою. Починаючи з лівого нижнього кута сітки, ви переміщаєте олівець до правого верхнього кута, стежачи за тим, щоб він залишався на лініях і рухався тільки вправо або вгору. Результат показаний зліва:

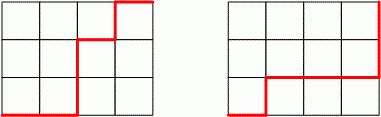
Дійсно шедевр, чи не так? Повторюючи процедуру ще раз, ви отримаєте зображення, показане праворуч. Тепер виникає питання: скільки різних витворів мистецтва можна таким чином створити?

Вхідні дані. Два натуральні числа $n$ і $m$ .

Вихідні дані. Виведіть кількість різних витворів мистецтва, які можна створити, використовуючи описану вище процедуру. Можна стверджувати, що це число відповідає $64$ — бітовому знаковому цілому числу.

Відкрити задачу

Гуннар — досить старий і забудькуватий дослідник. Зараз він пише статтю про безпеку в соціальних мережах, яка включає в себе деякі елементи комбінаторики. Він написав програму для обчислення біноміальних коефіцієнтів, щоб перевірити деякі розрахунки.

Біноміальний коефіцієнт $C_{n}^{k}$ — це число

C_{n}^{k} = \frac{n !}{k ! \cdot ( n - k )!}

де $n$ і $k$ — невід'ємні числа.

Гуннар використовує свою програму для обчислення $C_{n}^{k}$ і отримав число $m$ як результат. На жаль, оскільки він забудькуватий, він забув числа $n$ і $k$ , які він використовував як вхідні дані. Ці два числа були результатом довгих обчислень, і вони були записані на одному з численних аркушів, що лежать на його столі. Замість того щоб шукати в паперах, він вирішив відновити числа $n$ і $k$ за отриманою відповіддю. Чи можете ви допомогти йому знайти всі такі можливі значення?

Вхідні дані. Перша строка містить кількість тестів, не більше $100$ . Кожен тест задається в одній строкі і містить ціле число $m (2 \leq m \leq 1 0^{15})$ — результат програми Гуннара.

Вихідні дані. Для кожного тесту виведіть дві строки. Перша строка повинна містити кількість способів виразити $m$ за допомогою біноміального коефіцієнта. У другій строкі повинні розташовуватись всі пари $(n, k)$ , що задовольняють $C_{n}^{k} = m$ . Пари слід розташувати за зростанням $n$ , а у випадку рівності за зростанням $k$ . Формат виводу пар наведено в прикладі.

Відкрити задачу

Якщо $C_{n}^{k} = m$ , то $C_{n}^{n - k} = m$ . Достатньо знайти розв'язок $k \leq n /2$ і разом з парою $(k, n)$ вивести також пару $(k, n - k)$ . При $k = n /2$ ці дві пари співпадають.

Нехай $p$ — найменше число, для якого $C_{2 p}^{p} > m$ . Тоді очевидно що $0 \leq k < p$ .

Зафіксуємо таке $k$ що $C_{2 k}^{k} \leq m$ і розглянемо функцію $f (n) = C_{n}^{k}$ . Тоді при $2 k \leq n \leq m$ функція $f (n)$ є монотонно зростаючою. Відповідно можна розв'язати рівняння $f (n) = m$ бінарним пошуком.

Таким чином для розв'язання задачі слід перебрати значення $k (0 \leq k < p)$ і для кожного такого $k$ розв'язати рівняння $C_{n}^{k} = m$ щодо $n$ бінарним пошуком. Знайдене значення $n$ повинно бути цілочисельним.

Приклад

Розглянемо рівняння $C_{n}^{k} = 3003$ . Зважаючи на те що $C_{12}^{6} = 924$ , а $C_{14}^{7} = 3432$ , то нам достатньо перебрати $0 \leq k \leq 6$ .

Нехай $k = 2$ , розглянемо рівняння $C_{n}^{2} = 3003$ або $\frac{n \cdot ( n - 1 )}{2} = 3003$ , $n \cdot (n -1) = 6006$ . Бінарним пошуком в проміжку $4 \leq n \leq 3003$ знаходимо цілочисельне розв'язання $n = 78$ . Зважаючи на те що $n \neq = 2 \cdot k$ , маємо два розв'язки: $C_{78}^{2} = C_{78}^{76} = 3003$ .

Шукані пари будемо зберігати у векторі пар $res$ .

vector<pair<long long,long long> > res;

Функція Cnk обчислює значення біноміального коефіцієнта $C_{n}^{k}$ .

long long Cnk(long long n, long long k)
{
  long long i, Res = 1;
  if (k > n - k) k = n - k;
  for(i = 1; i <= k; i++)
  {

Якщо на черговій ітерації результат перевищує $m$ (ми шукаємо розв'язок рівняння $C_{n}^{k} = m$ ), то зупиняємось. Таким виходом з функції ми також уникнемо переповнення.

    if (1.0 * Res * (n - i + 1) / i > m) return m + 1;
    Res = Res * (n - i + 1) / i;
  }
  return Res;
}

Основна частина програми. Читаємо вхідні дані.

scanf("%d",&tests);
while (tests--) 
{
  res.clear();
  scanf("%lld",&m);

Перебираємо значення $k$ від $0$ до тих пір поки $C_{2 k}^{k} \leq m$ .

  for(k = 0; Cnk(2*k,k) <= m; k++)
  {

Шукаємо значення $n (2 k \leq n \leq m)$ бінарним пошуком.

    long long lo = 2*k, hi = m;
    while (lo < hi) 
    {
      long long n = (lo + hi) / 2;
      if (Cnk(n,k) < m) lo = n + 1; else hi = n;
    }

Якщо $C_{l o}^{k} = m$ , то розв'язок знайдено. Заносимо в результат одну або дві пари розв'язків.

    if (Cnk(lo,k) == m)
    {
      res.push_back(make_pair(lo,k));
      if (lo != 2*k)
        res.push_back(make_pair(lo,lo - k));
    }
  }

Сортуємо пари.

  sort(res.begin(),res.end());

Виводимо відповідь — кількість знайдених пар і самі пари.

  printf("%d\n",res.size());
  for(i = 0; i < res.size(); i++)
    printf("(%lld,%lld) ", res[i].first,res[i].second);
  printf("\n");
}

Асимптотичні оцінки для біноміального коефіцієнта

Теорема 1. Між біноміальними коефіцієнтами має місце співвідношення:

C_{n}^{0} < C_{n}^{1} < ... < C_{n}^{⌊ n /2 ⌋} \geq C_{n}^{⌊ n /2 ⌋ + 1} > ... > C_{n}^{n}

Теорема 2. $C_{2 n}^{n} < 4^{n}$ . Слід із того, що $\sum_{k = 0}^{2 n} C_{2 n}^{k} = (1 + 1)^{2 n} = 2^{2 n} = 4^{n}$

Теорема 3. $C_{2 n}^{n} > \frac{4 ^{n}}{2 n + 1}$ . Слід із того, що $\sum_{k = 0}^{2 n} C_{2 n}^{k} = 4^{n}$ , а самих коефіцієнтів $2 n + 1$ . Тому більший з коефіцієнтів буде більшим $\frac{4 ^{n}}{2 n + 1}$ .

Теорема 4. Формула Стірлінга. $n! \approx 2 πn (\frac{n}{e})^{n}$ .

Більш точне наближення має вигляд:

n! \approx 2 πn (\frac{n}{e})^{n} (1 + \frac{1}{12 n} + \frac{1}{288 n ^{2}} - \frac{139}{51849 n ^{3}} - \frac{571}{2488320 n ^{4}})

Теорема 5.

C_{2 n}^{n} \approx \frac{4 πn ( \frac{2 n}{e} ) ^{2 n}}{( 2 πn ( \frac{n}{e} ) ^{n} ) ^{2}} = \frac{4 ^{n}}{пі n}

Теорема 6.

C_{n}^{k} = \frac{n !}{k ! ( n - k )!} = \frac{n \cdot ( n - 1 ) \cdot ( n - 2 ) \cdot ... \cdot ( n - k + 1 )}{1 \cdot 2 \cdot 3 \cdot ... \cdot k} =

\frac{n !}{k !} \cdot (1 - \frac{1}{n}) \cdot (1 - \frac{2}{n}) \cdot ... \cdot (1 - \frac{k - 1}{n}) =

\frac{n !}{k !} \cdot e^{l n (1 - \frac{1}{n}) + l n (1 - \frac{2}{n}) + ... + l n (1 - \frac{k - 1}{n})} \leq (скористаємося нерівністю l n (1 - x) \leq - x)

\frac{n !}{k !} \cdot e^{- \frac{1}{n} - \frac{2}{n} - ... - \frac{k - 1}{n}} = \frac{n !}{k !} \cdot e^{- \frac{k \cdot ( k - 1 )}{2 n}}

Список використаних задач

Коментарі

Покищо нічого

Будьте першим, хто розпочне обговорення!

Увійти

Завантаження

Секундочку, отримую дані з серверу