Rekursiya və İterasiya
Proqramlaşdırmanın əsaslarını öyrənməyə başlayanda, adətən, ilk yazdığımız proqram "Hello, world!" sətirini çap edir. Sonra dəyişənlər, operatorlar, funksiyalarla tanış oluruq. Və adətən, bir başlanğıcçı ilk tanış olduğu operatorlar şərt operatoru və dövr operatorudur. Dərhal, bəzi sadə funksiya yazmaq istəyi yaranır: bir ədədin faktorialı, qüvvətə yüksəltmək, və ya binomial əmsalın hesablanması. Çox hallarda, bir başlanğıc proqramçı funksiyaların iterativ versiyasını həyata keçirir. Lakin, az adam bilir ki, hər hansı iterativ funksiya həmçinin rekursiv olaraq da həyata keçirilə bilər.
Rekursiya - proqramın (və ya funksiyanın) özünü birbaşa və ya digər proqramlar (funksiyalar) vasitəsilə çağırması ilə məlumatların emal təşkilatının bir üsuludur.
Bir funksiya rekursiv adlanır əgər, onun emalı zamanı, birbaşa və ya dolayısıyla, digər funksiyaların çağırışları zəncirinə vasitəsilə yenidən çağırılır.

Iterasiya - bəzi əməliyyatların təkrarlanaraq icra edildiyi, lakin rekursiv proqramların (funksiyaların) çağırışlarına səbəb olmayan məlumatların emal təşkilatının bir üsuludur.
Teorem. Hər hansı bir alqoritm rekursiv formada həyata keçirilə bilərsə, iterativ formada da yenidən yazıla bilər və əksinə.
Aşağıda, dövr operatorlarından və rekursiv yanaşmadan istifadə edərək həyata keçirilmiş bir sıra elementar funksiyaları nəzərdən keçirəcəyik. Hər hansı bir proqramlaşdırma dilində rekursiv funksiyaları yazmadan əvvəl, adətən, funksiyaların hesablanma metodunu müəyyən edən bir rekursiya əlaqəsi yazmaq lazımdır. Rekursiya əlaqəsi ən azı iki şərt ehtiva etməlidir:
I) rekursiyanın davam etdirilməsi şərti (rekursiya addımı);
II) rekursiyanın bitməsi şərti.
Rekursiya, funksiyanın özünə çağırışı ilə həyata keçiriləcək. Bu halda, rekursiyanın davam etdirilməsi şərti funksiyanın bədənində ilk növbədə yoxlanılmalıdır. Əgər bu doğrudursa, onda funksiyadan çıxırıq. Əks halda, rekursiv addım edirik.
Funksiyaların iterativ versiyası for dövr operatorundan istifadə edilərək həyata keçiriləcək.
1. Bir ədədin faktorialı. Mənfi olmayan tam ədəd -in faktorialı 1-dən -ə qədər bütün təbii ədədlərin hasilidir və ! ilə işarə olunur. Əgər !, onda aşağıdakı rekursiya əlaqəsi tutulur:
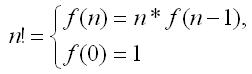
Birinci tənlik rekursiyanın addımını – -in vasitəsilə hesablanma metodunu təsvir edir. İkinci tənlik funksiyanın hesablanmasının nə zaman dayandırılacağını göstərir. Əgər müəyyən edilməsə, onda funksiya sonsuz işləyəcək.
Məsələn, dəyəri aşağıdakı kimi hesablanıla bilər:
Aydındır ki, -i hesablamaq üçün rekursiv çağırış etmək lazımdır.
rekursiv həyata keçirilmə | dövri həyata keçirilmə |
|---|---|
|
|
Dövri həyata keçirilmənin ideyası bir ədədin faktorialını dövr operatorundan istifadə edərək birbaşa hesablamaqdır:
2. Bir ədədin qüvvəti xətti zamanda. Bir ədədin qüvvətini xətti (O()) zaman qiymətləndirməsi ilə hesablamaq aşağıdakı rekursiya əlaqəsi ilə müəyyən edilə bilər:
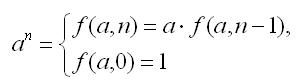
rekursiv həyata keçirilmə | dövri həyata keçirilmə |
|---|---|
|
|
İterativ versiyada, kifayətdir ki, ( ədəd amili) hasilini hesablayaq.
3. Bir ədədin qüvvəti loqarifmik zamanda. Bir ədədin qüvvətini zaman qiymətləndirməsi O(log) olaraq müəyyən edilir:
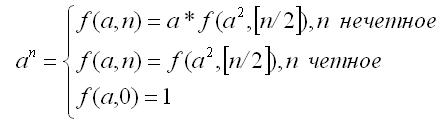
Məsələn, onuncu qüvvətə yüksəltmək belə həyata keçirilə bilər:
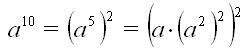
Kvadrata yüksəltmək bir çarpmanı təmsil etdiyi üçün, -u hesablamaq üçün 4 çarpma kifayətdir.
rekursiv həyata keçirilmə | dövri həyata keçirilmə |
|---|---|
|
|
4. Bir ədədin rəqəmlərinin cəmi. Təbii ədəd -in rəqəmlərinin cəmi funksiyası ilə aşağıdakı kimi tapıla bilər:
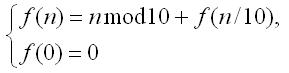
Rekursiyanın davam etdirilməsi şərti: bir ədədin rəqəmlərinin cəmi o ədədin son rəqəmi ilə son rəqəmi olmayan ədədin (ədəd 10-a bölünmüşdür) rəqəmlərinin cəminə bərabərdir.
Rekursiyanın bitməsi şərti: Əgər ədəd 0-dırsa, onda onun rəqəmlərinin cəmi 0-dır.
Məsələn, 234 ədədinin rəqəmlərinin cəmi aşağıdakı kimi hesablanacaq:
rekursiv həyata keçirilmə | dövri həyata keçirilmə |
|---|---|
|
|
5. Birliklərin sayı. Ədədin ikilik təmsilindəki birliklərin sayı funksiyası ilə aşağıdakı kimi hesablanıla bilər (& - bitvi 'VƏ' əməliyyatı):
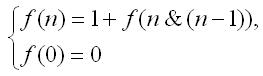
Əməliyyat n = n & (n – 1) nəticəsində ədədin ikilik təmsilindəki son birlik məhv edilir:
n & (n – 1) = a_1a_2…a_{k-1} 000…0
Funksiyanın rekursiv çağırışı ədədin ikilik təmsilindəki birliklərin sayı qədər ediləcək.
rekursiv həyata keçirilmə | dövri həyata keçirilmə |
|---|---|
|
|
6. Binomial əmsal. Binomial əmsalın dəyəri
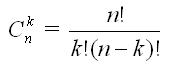
aşağıdakı rekursiya əlaqəsi ilə müəyyən edilir:
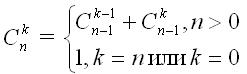
int c(int k, int n){ if (n == k) return 1; if (k == 0) return 1; return c(k - 1, n - 1) + c(k, n - 1);}
Nəzərə alaraq ki,
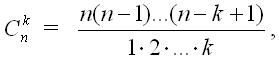
binomial əmsalın dəyəri dövr vasitəsilə hesablana bilər. Bu halda, bütün bölünmə əməliyyatları tam olacaq. Əgər , onda hesablama zamanı Məhdudiyyət Zamanını keçməmək üçün
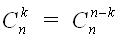
münasibətindən istifadə edin.
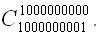
int Cnk(int k, int n){ long long res = 1; if (k > n - k) k = n - k; for (int i = 1; i <= k; i++) res = res * (n - i + 1) / i; return (int)res;}
7. Rekursiv funksiya. Verilmiş təbii üçün funksiyasının dəyərini aşağıdakı rekursiya əlaqələri ilə hesablayaq:
Funksiyanın birbaşa həyata keçirilməsi belədir:
int f(int n){ if (n <= 1) return n; if (n % 2) return f(n / 2) + f(n / 2 + 1); return f(n / 2);}
Bu həyata keçirilmədə, funksiyasının bəzi dəyərləri bir neçə dəfə hesablanıla bilər. -in dəyərlərini hesablamaq üçün başqa bir yanaşmanı nəzərdən keçirək. Funksiyanı
üçün aşağıdakı bərabərliklər tutulur:
Verilən əlaqələrdən istifadə edərək, dəyəri zaman qiymətləndirməsi O(log ) ilə hesablana bilər.
int g(int n, int i, int j){ if (!n) return j; if (n % 2) return g(n / 2, i, i + j); return g(n / 2, i + j, j);}
int f(int n){ return g(n, 1, 0);}
8. Ackermann funksiyası. Ackermann funksiyası A(, ) aşağıdakı kimi rekursiv olaraq müəyyən edilir:
A(0, ) = + 1,
A(, 0) = A( – 1, 1),
A(, ) = A( – 1, A(, – 1))
Ackermann funksiyasının rekursiv həyata keçirilməsi belədir:
int a(int m, int n){ if (!m) return n + 1; if (!n) return a(m - 1, 1); return a(m - 1, a(m, n - 1));}
Kiçik dəyərləri üçün, Ackermann funksiyası açıq şəkildə ifadə edilə bilər:
A(0, ) = + 1
A(1, ) = 2 + ( + 3) – 3 = + 2
A(2, ) = 2 · ( + 3) – 3 = 2 · + 3
A(3, ) = 2 – 3
9. Kəşfiyyat üçün seçim [ACM, 1999]. Sıraya düzülmüş əsgərdən bir neçəsini kəşfiyyata seçmək lazımdır. Bunun üçün aşağıdakı əməliyyat icra edilir: əgər sırada 3-dən çox əsgər varsa, onda cüt mövqelərdə dayanan bütün əsgərlər çıxarılır, və ya tək mövqelərdə dayanan bütün əsgərlər çıxarılır. Bu prosedur sırada 3 və ya daha az əsgər qalana qədər təkrarlanır. Onlar kəşfiyyata göndərilirlər. Bu cür kəşfiyyat qruplarının yaradılma yollarının sayını hesablayın.
Giriş. Sırada dayanan əsgərlərin sayı (0 < ≤ 10).
Çıxış. Əsgərlərin yuxarıda göstərilən şəkildə kəşfiyyata seçilmə yollarının sayı.
Nümunə giriş | Nümunə çıxış |
|---|---|
|
|
|
|
Həll. ilə sırada dayanan adamdan kəşfiyyat qruplarının yaradılma yollarının sayını işarə edək. Yalnız üç kəşfiyyatçıdan maraqlandığımız üçün, , , . Yəni, üç adamdan yalnız bir qrup yaradıla bilər, bir və ya iki adamdan heç biri.
Əgər cütdürsə, onda problemə görə sırada dayanan əsgərləri çıxardıqdan sonra, ya cüt mövqelərdə dayanan / 2 əsgər, ya da tək mövqelərdə dayanan / 2 əsgər qalacaq. Beləliklə, cüt üçün .
Əgər təkdirsə, onda çıxarmaqdan sonra, ya cüt mövqelərdə dayanan / 2 əsgər, ya da tək mövqelərdə dayanan / 2 + 1 əsgər qalacaq. Tək üçün cəmi yolların sayı bərabərdir
Beləliklə, -in dəyərini hesablamaq üçün əldə edilmiş rekursiya formulunu:
, əgər cütdürsə
, əgər təkdirsə
funksiyasının həyata keçirilməsi belədir:
int f(int n){ if (n <= 2) return 0; if (n == 3) return 1; if (n % 2) return f(n / 2) + f(n / 2 + 1); return 2 * f(n / 2);}
MƏNBƏLƏR
"Alqoritmlər: Dizayn və Analiz", Cormen T., Leiserson C., Rivest R., Stein C., – Moskva, Sankt-Peterburq, Kiyev, 2005 – 1292 s.
"Proqramlaşdırmanın Praktikası və Teorisi", Kitab2. "Proqramlaşdırmanın Praktikası və Teorisi", Cild 2. Vinokurov N.A., Vorozhtsov A.V., - Moskva: Fizmatkniga, 2008 - 288 s.