Перестановки дерев**і**в

Одного разу містер Кул створив дерево (неорієнтований зв'язний граф без циклів) з n вершин, призначивши кожній вершині i > 1 два числа: p[i] < i - прямий предок вершини i і w[i] - вага ребра між вершиною i та p[i]. Вершина 1 є коренем, тому у неї немає предків.

Ви хотіли дізнатися, яке дерево побудував містер Кул, але він відмовився це сказати, хоча й дав вам підказку:

Він записав наступні числа в одному рядку, отримавши масив b довжини 2 * n - 2.

b = [p[2], w[2], p[3], w[3], ..., p[n-1], w[n-1], p[n], w[n]]

Потім він випадково перемішав його, отримавши масив a, і передав його вам. Оскільки відновити дерево, знаючи лише значення масиву a, неможливо, вам довелося вирішити інше завдання.

Назвемо дерево k-довгим, якщо на шляху між вершинами 1 і n розташовано рівно k ребер.

Назвемо дерево k-досконалим, якщо воно k-довге і сума ваг ребер на шляху між вершиною 1 і вершиною n максимальна серед усіх можливих k-довгих дерев, які міг побудувати містер Кул.

Вам слід вивести суму ваг ребер на шляху між вершиною 1 і вершиною n для всіх можливих k-досконалих дерев. Виведіть -1, якщо містер Кул не може побудувати якесь k-довге дерево.

Вхідні дані

Перша строка містить одне ціле число n (2 ≤ n ≤ 10^5) - кількість вершин у дереві.

Друга строка містить 2 * n - 2 цілих чисел a[1], a[2], ..., a[2n-2] (1 ≤ a[i] ≤ n - 1) - елементи масиву a.

Вихідні дані

В одному рядку виведіть n - 1 цілих чисел w[1], w[2], w[3], ..., w[n-1], де w[k] — сума ваг ребер на шляху між вершиною 1 і вершиною n в k-досконалому дереві. Якщо i-довгого дерева немає, то w[i] має дорівнювати -1.

Приклади

Примітка

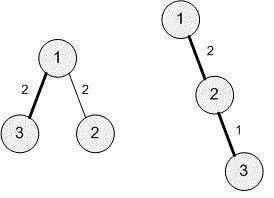
У першому прикладі 1-досконале дерево визначається масивом [1, 2, 1, 2] (тобто p[2] = 1, w[2] = 2, p[3] = 1, w[3] = 2).

2-досконале дерево визначається масивом [1, 2, 2, 1] (тобто p[2] = 1, w[2] = 2, p[3] = 2, w[3] = 1). Нижче наведені ілюстрації 1-досконалого дерева і 2-досконалого дерева відповідно (шлях від вершини 1 до вершини n намальований жирними лініями):

У другому прикладі немає k-досконалих дерев, які можна отримати перестановкою масиву a.

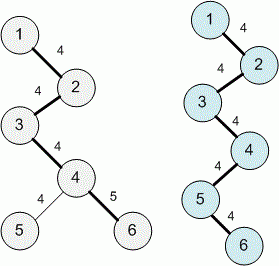
У третьому прикладі можна отримати лише 4-досконале дерево і 5-досконале дерево. Вони визначаються масивами [1, 4, 2, 4, 3, 4, 4, 4, 4, 5] і [1, 4, 2, 4, 3, 4, 4, 4, 5, 4] відповідно. Ось ілюстрації до них: