Розбір

Let $f(a,b)$ be the minimum number of moves required to cut a rectangle of size $a\times b$ into squares. We'll store this value in the cell $dp[a][b]$.

If the rectangle is already a square $(a=b)$, no cuts are needed, so $f(a,a)=0$.

A rectangle $a\times b$ can be cut either vertically or horizontally. Let's first consider a vertical cut.

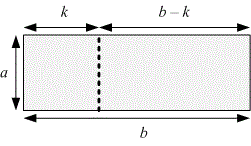
With a vertical cut, the rectangle $a\times b$ is divided into two rectangles: $a\times k$ and $a\times (b-k)$. For the resulting rectangles to be non-degenerate, the condition $1\le k<b$ must hold. Then recursively solve the problem for each of these two rectangles and add $1$ to the result, as we made one vertical cut. We choose such a $k$ that minimizes the sum $f(a,k)+f(a,b-k)+1$:

For a horizontal cut, we get a similar formula:

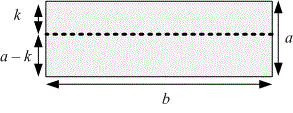
It remains to choose the minimum value among these two options.

Example

In the first test, $3$ cuts are required:

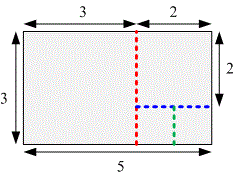
• The first cut divides the $3\times 5$ rectangle into $3\times 3$ and $2\times 3$;

• The second cut divides the $2\times 3$ rectangle into $2\times 2$ and $2\times 1$;

• The third cut divides the $2\times 1$ rectangle into $1\times 1$ and $1\times 1$;

Algorithm implementation

Let’s declare constants and the array.

#define MAX 501
#define INF 0x3F3F3F3F

int dp[MAX][MAX];

The function $f(a,b)$ returns the minimum number of moves required to cut a rectangle of size $a\times b$ into squares.

int f(int a, int b)
{

If the rectangle is already a square $(a=b)$, no cuts are needed.

  if (a == b) return 0;

If the value of $f(a,b)$ is not computed $(dp[a][b]=\infty )$, compute it.

  if (dp[a][b] == INF)
  {

Perform all possible vertical cuts.

    for (int k = 1; k < b; k++)
      dp[a][b] = min(dp[a][b], f(a, k) + f(a, b - k) + 1);

Perform all possible horizontal cuts.

    for (int k = 1; k < a; k++)
      dp[a][b] = min(dp[a][b], f(k, b) + f(a - k, b) + 1);
  }

Return the result $f(a,b)=dp[a][b]$.

  return dp[a][b];
}

The main part of the program. Read the dimensions of the rectangle $a$ and $b$.

scanf("%d %d", &a, &b);

Compute and print the answer.

memset(dp, 0x3F, sizeof(dp));
printf("%d\n", f(a, b));