Не такий вже й плоский

Будь-яке додатне ціле число v можна представити у вигляді p_1^a1*p_2^a2*...*p_n^an, де p_i — просте число, а a_i ≥ 0. Наприклад: 24 = 2^3*3^1.
Виберіть будь-які два простих числа p_1 та p_2, де p_1 ≠ p_2. Уявіть двовимірну площину, де степені p_1 відкладені на осі x, а степені p_2 на осі y. Тепер будь-яке число, яке можна записати як p_1^a1*p_2^a2, може бути відображене на цій площині в точці (x, y) = (a_1, a_2). На рисунку праворуч показано кілька прикладів, де p_1 = 3 та p_2 = 2.
Цю ідею можна розширити на будь-який N-вимірний простір, де кожній з N осей присвоєно унікальне просте число. Кожен N-вимірний простір має унікальний набір простих чисел. Ми називаємо такий набір Набором Ідентифікації Простору або скорочено S. |S| (порядок S) є N.
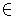
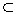
Будь-яке число, яке може бути виражене як добуток p_iS (кожне піднесене до степеня (a_i ≥ 0), може бути відображене в цьому |S|-вимірному просторі. Малюнок внизу ілюструє цю ідею для N = 3 та S = {2, 3, 7}. Зрозуміло, що будь-яке число, яке може бути відображене в просторі A, може також бути відображене в просторі B, якщо S_A ⊆ S_B.
Ми визначаємо відстань між будь-якими двома точками в заданому N-вимірному просторі як суму одиниць, пройдених для переходу від однієї точки до іншої, слідуючи лініям сітки (тобто рух завжди паралельний одній з осей). Наприклад, на рисунку нижче відстань між 168 та 882 дорівнює 4.
Дано два додатні цілі числа, напишіть програму, яка визначає мінімальний порядок простору, де обидва числа можуть бути відображені. Програма також визначає відстань між цими двома числами в цьому просторі.

Вхідні дані
Ваша програма буде протестована на одному або більше тестових випадках. Кожен тестовий випадок задається на рядку з двома додатними цілими числами (0 < A, B < 1, 000, 000), де A*B > 1.
Останній рядок складається з двох нулів.
Вихідні дані
Для кожного тестового випадку виведіть наступний рядок:
k. X:D
Де k — номер тестового випадку (починаючи з одиниці), X — мінімальний порядок, необхідний у просторі, де обидва A та B можуть бути відображені. D — відстань між цими двома точками.
Примітка: Перед X є пробіл.