Аналіз алгоритму

Позначимо через $f(n)$ кількість шуканих послідовностей з 0 і 1 довжини $n$. Якщо на першому місці послідовності знаходиться 0, то, починаючи з другого місця, можна побудувати $f(n-1)$ послідовність. Якщо на першому місці стоїть 1, то на другому місці можливі обидва варіанти. Якщо там стоїть 0, то на наступних $n-2$ вільних місцях можна побудувати $f(n-2)$ послідовностей. Якщо 1, то на третьому місці обов'язково повинен знаходитися 0 і, починаючи з четвертого місця, можна побудувати $f(n-3)$ послідовностей.

Маємо рекурентне співвідношення: $f(n)=f(n-1)+f(n-2)+f(n-3)$. Залишається обчислити початкові значення:

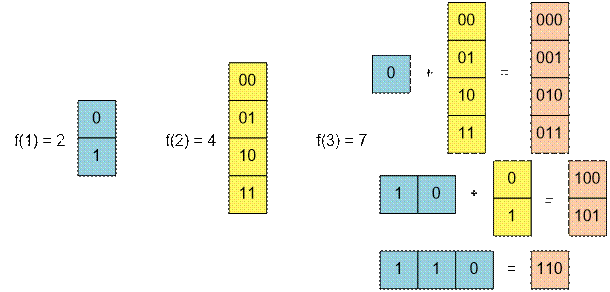
• $f(1)=2$, оскільки існує дві послідовності довжини 1: 0 і 1.

• $f(2)=4$, оскільки існує чотири послідовності довжини 2: 00, 01, 10 і 11.

• $f(3)=7$, оскільки існує сім послідовностей довжини 3: 000, 001, 010, 011, 100, 101 і 110.

Приклад

Реалізація алгоритму

Оголосимо масив f, в якому будемо зберігати значення f(1), f(2), …, f(n).

int f[100010];

Читаємо вхідне значення n.

scanf("%d",&n);

Заносимо в відповідні комірки масиву f значення f(1), f(2) і f(3).

f[1] = 2; f[2] = 4; f[3] = 7;

Обчислюємо значення f(i) за рекурентною формулою. Обчислення проводимо за модулем 12345.

for(i = 4; i <= n; i++)
    f[i] = (f[i-1] + f[i-2] + f[i-3]) % 12345;

Виводимо відповідь.

printf("%d\n",f[n]);

Реалізація алгоритму – рекурсія + запам'ятовування

Оголосимо масив dp для запам'ятовування результатів: dp[i] буде зберігати значення f(i).

int dp[100001];

Реалізуємо функцію f(n) – кількість шуканих послідовностей з 0 і 1 довжини n. Використовуємо техніку мемоізації.

int f(int n)
{
    if (n == 1) return 2;
    if (n == 2) return 4;
    if (n == 3) return 7;
    if (dp[n] != -1) return dp[n];
    return dp[n] = (f(n-1) + f(n-2) + f(n-3)) % 12345;
}

Основна частина програми. Читаємо вхідне значення n.

scanf("%d",&n);

Ініціалізуємо масив dp.

memset(dp,-1,sizeof(dp));

Обчислюємо і виводимо значення f(n).

printf("%d\n",f(n));

Java реалізація

import java.util.*;

public class Main
{
    public static int MAX = 100010;
    static int f[] = new int[MAX];

    public static void main(String[] args)
    {
        Scanner con = new Scanner(System.in);
        int n = con.nextInt();
        f[1] = 2; f[2] = 4; f[3] = 7;
        for(int i = 4; i <= n; i++)
            f[i] = (f[i-1] + f[i-2] + f[i-3]) % 12345;
        System.out.println(f[n]);
        con.close();
    }
}

Python реалізація

n = int(input())

dp = [0] * (n + 4)
dp[1], dp[2], dp[3] = 2, 4, 7

for i in range(4, n + 1):
    dp[i] = (dp[i-1] + dp[i-2] + dp[i-3]) % 12345;

print(dp[n])

Python реалізація – рекурсія з запам'ятовуванням

Збільшимо стек для рекурсії.

import sys
sys.setrecursionlimit(10000)

def f(n):
    if n == 1: return 2
    if n == 2: return 4
    if n == 3: return 7
    if dp[n] != -1: return dp[n]

    dp[n] = (f(n - 1) + f(n - 2) + f(n - 3)) % 12345
    return dp[n]

n = int(input())

dp = [-1] * 100001

print(f(n))