Розбір

Sort the roads (edges of the graph) in ascending order of danger. To solve the problem, we'll use a disjoint-set (union-find) data structure. Initially, we form $n$ sets, each containing one vertex. Iterate over the edges in ascending order of danger. For each edge $(a, b)$ , merge the sets containing vertices $a$ and $b$ . Once vertices $1$ and $n$ belong to the same set, the algorithm terminates. At that point, a path from vertex $1$ to vertex $n$ will exist, and the danger of the roads on this path will not exceed the danger of the last edge considered.

Thus, if after processing edge $(x, y)$ , the representatives of vertices $1$ and $n$ coincide, the danger of the safest route will be equal to the danger of road $(x, y)$ .

Example

In the first test case, the danger of the safest route is $1$ .

Consider the second test case.

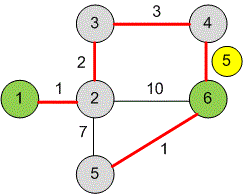
The edges are processed in ascending order of their danger. Once an edge with a danger of $5$ is processed, vertices $1$ and $6$ will be connected, and the algorithm will terminate.

Algorithm implementation

Declare an array $ma s$ , used by the disjoint-set system. The edges of the graph will be stored in array $e$ .

#define MAX 1000001
int mas[MAX];
struct Edge
{
  int x, y, danger;
} e[MAX];

The Repr function finds the representative of the set containing vertex $n$ . To avoid a Time Limit verdict, a heuristic is used: if the representative of vertex $n$ is $x$ , then $ma s [n]$ should be set to $x$ .

int Repr(int n)
{
  if (n == mas[n]) return n;
  return mas[n] = Repr(mas[n]);
}

The Union function merges the sets containing vertices $x$ and $y$ .

int Union(int x,int y)
{
  int x1 = Repr(x),y1 = Repr(y);
  mas[x1] = y1;
  return (x1 != y1);
}

Declare a comparator lt for comparing edges. The roads are sorted in ascending order of their danger.

int lt(Edge a, Edge b)
{
  return (a.danger < b.danger);
}

The main part of the program. Read the number of cities $n$ and roads $m$ .

scanf("%d %d",&n,&m);

Initialize the array $ma s$ .

for(i = 1; i <= n; i++) mas[i] = i;

Read the edges of the graph into the array $e$ .

for(i = 0; i < m; i++)
  scanf("%d %d %d",&e[i].x,&e[i].y,&e[i].danger);

Sort the edges in ascending order of danger.

sort(e,e+m,lt);

Iterate through the edges, starting from the least dangerous one. Merge the sets containing their vertices. Once vertices $1$ and $n$ are in the same set ( $R e p r (1)$ becomes equal to $R e p r (n)$ ), the safest path will be found. Its danger will be equal to the danger of the last processed edge, that is, $e [i] . d an g er$ .

for(i = 0; i < m; i++)
{
  Union(e[i].x,e[i].y);
  if (Repr(1) == Repr(n)) break;
}

Print the answer.

printf("%d\n",e[i].danger);

Java implementation

import java.util.*;

class Edge
{
  int x, y, danger;
  Edge (int x, int y, int danger)
  {
    this.x = x;
    this.y = y;
    this.danger = danger;
  }
};

public class Main
{
  static int mas[], size[];
	
  static int Repr(int n)
  {
    if (n == mas[n]) return n;
    return mas[n] = Repr(mas[n]);
  }
	
  static boolean Union(int x,int y)
  {
    x = Repr(x); y = Repr(y);
    if(x == y) return false;

    if (size[x] < size[y])
    {
      int temp = x; x = y; y = temp;
    }
    mas[y] = x;
    size[x] += size[y];
    return true;    
  }
  
  public static class MyFun implements Comparator<Edge>
  {
    public int compare(Edge a, Edge b)
    {
      return a.danger - b.danger;
    }
  }
  
  public static void main(String[] args)
  {
    Scanner con = new Scanner(System.in);
    int n = con.nextInt();
    int m = con.nextInt();
    mas = new int[n+1];
    size = new int[n+1];
    
    for(int i = 1; i <= n; i++)
    {
      mas[i] = i;
      size[i] = 1;
    }
    
    Vector<Edge> v = new Vector<Edge>();
    for(int i = 0; i < m; i++)
    {
      int x = con.nextInt();
      int y = con.nextInt();
      int dust = con.nextInt();
      v.add(new Edge(x,y,dist));
    }

    Collections.sort(v, new MyFun());
    
    int index = 0;
    for(int i = 0; i < m; i++)
    {
      Union(v.get(i).x,v.get(i).y);
      if (Repr(1) == Repr(n)) 
      {
        index = i;
        break;
      }
    }
    
    System.out.println(v.get(index).danger);
    con.close();
  }
}

Python implementation

Declare the structure $E d g e$ for an edge.

class Edge:
  def __init__(self, x, y, danger):
    self.x = x
    self.y = y
    self.danger = danger

def Repr(n):
  if n == mas[n]:
    return n
  mas[n] = Repr(mas[n])
  return mas[n]

The Union function merges the sets containing vertices $x$ and $y$ .

def Union(x, y):
  x1 = Repr(x)
  y1 = Repr(y)
  mas[x1] = y1
  return x1 != y1

The main part of the program. Read the number of cities $n$ and roads $m$ .

n, m = map(int, input().split())

Initialize the list $ma s$ , used by the disjoint-set system.

mas = [i for i in range(n + 1)]

Read the edges of the graph into the list $e$ .

e = []
for i in range(m):
  x, y, danger = map(int, input().split())
  e.append(Edge(x, y, danger))

Sort the edges in ascending order of danger.

e.sort(key=lambda x: x.danger)

for i in range(m):
  Union(e[i].x, e[i].y)
  if Repr(1) == Repr(n):
    break

Print the answer.

print(e[i].danger)