Квадратний корінь (#3968)

Аналіз алгоритму

Розглянемо функцію $f (x) = x^{2} + x$ . Очевидно, що:

$f (0) = 0$ ;
$f (C) = C^{2} + C > C$ .

Тобто корінь рівняння

f (x) = С

лежить на проміжку $[0; C]$ . Функція $f (x)$ строго зростаюча. Шукаємо корінь $x$ бінарним пошуком.

Приклад

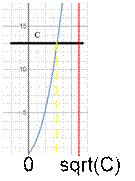
Розглянемо графік функції $f (x) = x^{2} + x$ . Можна помітити що:

$f (0) = 0 < C$ ;
$f (C) = C + C > C$ .

Отже корінь рівняння $f (x) = С$ лежить на проміжку $[0; C]$ і може бути знайдений бінарним пошуком.

Реалізація алгоритму

Оголосимо константу EPS і функцію f(x).

#define EPS 1e-10

double f(double x)
{
    return x * x + sqrt(x);
}

Основна частина програми. Читаємо значення $C$ .

scanf("%lf", &c);

Встановлюємо межі бінарного пошуку [left; right] = [0; C].

left = 0; right = c;

Запускаємо бінарний пошук.

while (right - left > EPS)
{
    middle = (left + right) / 2;
    y = f(middle);
    if (y > c) right = middle; else left = middle;
}

Виводимо відповідь.

printf("%lf\n", left);

Java реалізація

import java.util.*;

public class Main
{
    static double f(double x)
    {
        return x * x + Math.sqrt(x);
    }

    public static void main(String[] args)
    {
        Scanner con = new Scanner(System.in);
        double c = con.nextDouble();
        double left = 0, right = c;

        while (right - left > 1e-10)
        {
            double middle = (left + right) / 2;
            double y = f(middle);
            if (y > c) right = middle; else left = middle;
        }
        System.out.println(left);
        con.close();
    }
}