Метро

Аналіз алгоритму

Найкоротша відстань від джерела до вершини $v$ , що належить лінії $l$ , зберігаємо в dist[v][l], де $1 \leq v \leq 70, 1 \leq l \leq 10$ . Граф зберігаємо у вигляді списків суміжності. Разом з напрямком і вартістю ребра зберігаємо номер лінії метро, якій належить вершина, куди спрямоване ребро.

Починаємо зі станції $s$ , що знаходиться на лінії $l in e 1$ . Відповідь на задачу – мінімальна вартість, за яку можна дістатися до вершини $f$ на лінії $l in e 2$ . При русі між вершинами слід провести перевірку: якщо вершини належать різним лініям, то слід додати 1 (здійснити пересадку).

За допомогою алгоритму Дейкстри знаходимо найкоротші відстані зі стану ( $s$ , $l in e 1$ ) до ( $f$ , $l in e 2$ ).

Приклад

Граф, наведений у прикладі, має вигляд:

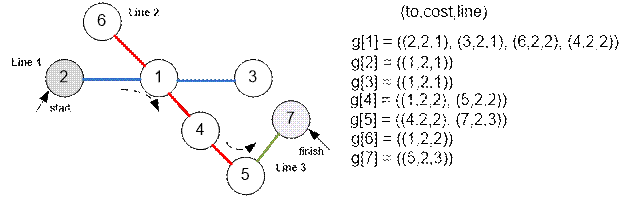
Для пересування зі станції 2 на станцію 7 необхідно проїхати 4 перегони (8 хвилин) і зробити 2 пересадки (2 хвилини). Всього час руху займе 10 хвилин.

Реалізація алгоритму

Кількість вершин у графі не більше MAX = 71. Кількість ліній не більше LINES = 11.

#define MAX 71
#define LINES 11

int dist[MAX][LINES];

struct node
{
    int to, cost, line;
    node(int to, int cost, int line) : to(to), cost(cost), line(line) {}
};

bool operator< (node a, node b)
{
    return a.cost > b.cost;
}

vector<vector<node>> g;

// Читання вхідних даних та ініціалізація графа

for (i = 1; i <= l; i++)
{
    scanf("%d ", &u);
    while (scanf("%d%c", &v, &ch))
    {
        g[u].push_back(node(v, 2, i));
        g[v].push_back(node(u, 2, i));
        u = v;
        if (ch == '\n') break;
    }
}

// Ініціалізація масиву найкоротших відстаней
for (i = 1; i <= n; i++)
    for (j = 1; j <= l; j++)
        dist[i][j] = 2000000000;

// Читання інформації про початкову та кінцеву станцію
scanf("%d %d %d %d", &s, &line1, &f, &line2);

// Алгоритм Дейкстри
dist[s][line1] = 0;
priority_queue<node, vector<node>> pq;
pq.push(node(s, 0, line1)); // (v, cost, line)

while (!pq.empty())
{
    int cost = pq.top().cost;
    int v = pq.top().to;
    int l1 = pq.top().line;
    pq.pop();

    for (i = 0; i < g[v].size(); i++)
    {
        int to = g[v][i].to;
        int w = g[v][i].cost;
        int l2 = g[v][i].line;
        int tot_cost = cost + w;
        if (l1 != l2) tot_cost += 1;
        if (tot_cost < dist[to][l2])
        {
            dist[to][l2] = tot_cost;
            pq.push(node(to, tot_cost, l2));
        }
    }
}

// Вивід відповіді
printf("%d\n", dist[f][line2]);