Сума на відрізку (#682)

Аналіз алгоритму

Кожен запит $S_{l, r}$ можна виконувати за допомогою циклу за час $O (n)$ . Існує $m \leq 1 0^{6}$ запитів, довжина масиву складає $n \leq 1 0^{6}$ . При лінійному часі виконання запиту нам потрібно не більше $n \times m \leq 1 0^{12}$ операцій, що дасть Time Limit.

Розглянемо часткові суми масиву $a$ : $s_{1} = a_{1};$ $s_{2} = a_{1} + a_{2};$ $s_{3} = a_{1} + a_{2} + a_{3};$ . . . $s_{n} = a_{1} + a_{2} + a_{3} + ... + a_{n};$

Обчислити значення $s_{1}, s_{2}, \dots, s_{n}$ можна в лінійному масиві $s$ за час $O (n)$ .

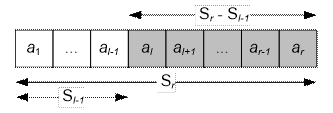
Далі помітимо, що $S_{l, r} = a_{l} + a_{l + 1} + \dots + a_{r} = (a_{1} + \dots + a_{l} + a_{l + 1} + \dots + a_{r}) - (a_{1} + \dots + a_{l - 1}) = s_{r} - s_{l - 1}$

Таким чином відповісти на запит $S_{l, r}$ можна за $O (1)$ , тобто за константний час.

Приклад

Обчислимо суму $a_{3} + a_{4} + a_{5}$ для наведеного в умові прикладу.

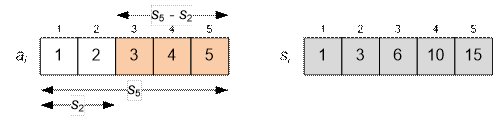
Маємо: $a_{3} + a_{4} + a_{5} = s_{5} - s_{2} = 15-3 = 12.$

Реалізація алгоритму

Оголосимо два робочих одновимірних масиви.

#define MAX 1000001
int a[MAX], s[MAX];

Читаємо вхідний набір чисел у масив a, обчислюємо часткові суми у масиві s.

scanf("%d",&n); s[0] = 0;
for(i = 1; i <= n; i++)
{
    scanf("%d",&a[i]);
    s[i] = s[i-1] + a[i];
}

Обробляємо $m$ запитів.

scanf("%d",&m);
for(i = 0; i < m; i++)
{
    scanf("%d %d",&b,&c);
    printf("%d\n",s[c] - s[b-1]);
}

Реалізація алгоритму – SQRT декомпозиція - TLE

#include <cstdio>
#include <cmath>
#include <vector>
using namespace std;

int i, n, m, len, x, y;
vector<int> a, b;

int q(int l, int r)
{
    int i, sum = 0;
    int c_l = l / len, c_r = r / len;
    if (c_l == c_r)
        for (i = l; i <= r; i++)
            sum += a[i];
    else
    {
        for (i = l; i <= (c_l + 1)*len - 1; i++)
            sum += a[i];
        for (i = c_l + 1; i <= c_r - 1; i++)
            sum += b[i];
        for (i = c_r * len; i <= r; i++)
            sum += a[i];
    }
    return sum;
}

int main(void)
{
    scanf("%d", &n);
    a.resize(n);
    for (i = 0; i < n; i++)
        scanf("%d", &a[i]);

    len = sqrt(n) + 1;
    b.resize(len);
    for (i = 0; i < n; i++)
        b[i / len] += a[i];

    scanf("%d", &m);
    for (i = 0; i < m; i++)
    {
        scanf("%d %d", &x, &y);
        printf("%d\n", q(x - 1, y - 1));
    }
    return 0;
}

Реалізація алгоритму – запит за лінійний час - TLE

#include <stdio.h>
#define MAX 1000001

int i, j, n, m, b, c, s;
int a[MAX];

int main(void)
{
    scanf("%d", &n);
    for (i = 1; i <= n; i++)
        scanf("%d", &a[i]);

    scanf("%d", &m);
    for (i = 0; i < m; i++)
    {
        scanf("%d %d", &b, &c);
        s = 0;
        for (j = b; j <= c; j++)
            s = s + a[j];
        printf("%d\n", s);
    }
    return 0;
}