Розбір

Let's build an adjacency matrix from the list of edges. Start a depth-first search from the specified vertex $v$ . Each time we enter a new vertex, we print its number.

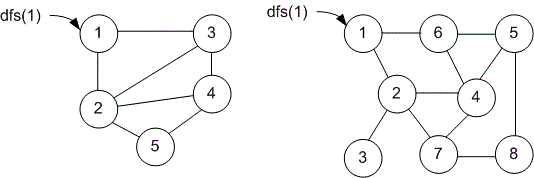
Exercise

Solve the problem for the next graphs:

Algorithm realization — adjacency matrix

Declare an adjacency matrix $g$ and an array $u se d$ .

#define MAX 101
int g[MAX][MAX], used[MAX];

The dfs function performs a depth-first search from vertex $v$ .

void dfs(int v)
{

Print the vertex $v$ .

  printf("%d ", v);

Mark the vertex $v$ as visited.

  used[v] = 1;

Iterate over the vertices $i$ , that can be reached from $v$ . Moving from $v$ to $i$ is possible if:

There is an edge $(v, i)$ , that is, $g [v] [i] = 1$ ;
The vertex $i$ is not visited $(u se d [i] = 0)$

If both conditions are true, we continue the depth-first search from vertex $i$ .

  for (int i = 1; i <= n; i++)
    if ((g[v][i] == 1) && (used[i] == 0)) dfs(i);
}

The main part of the program. Read the number of vertices $n$ and edges $m$ in the graph.

scanf("%d %d", &n, &m);}

Initialize the arrays with zeroes.

memset(g, 0, sizeof(g));
memset(used, 0, sizeof(used));

Read the list of edges. Construct the adjacency matrix.

for (i = 0; i < m; i++)
{
  scanf("%d %d", &a, &b);
  g[a][b] = g[b][a] = 1;
}

Read vertex $v$ and start a depth-first search from it.

scanf("%d", &v);
dfs(v);
printf("\n");

Algorithm realization — adjacency list

Declare an adjacency list $g$ and an array $u se d$ .

vector<vector<int> > g;
vector<int> used;

The dfs function performs a depth-first search from vertex $v$ .

void dfs(int v)
{

Mark the vertex $v$ as visited.

  used[v] = 1;

Print the vertex $v$ .

  printf("%d ", v);

The array $g [v]$ contains a list of vertices adjacent to $v$ . Iterate over the vertices $t o$ that can be reached from $v$ .

  for (int to : g[v])

Consider the edge $(v, t o)$ . We can move to vertex $t o$ from $v$ if the vertex $t o$ is not visited $(u se d [t o] = 0)$ .

    if (used[to] == 0) dfs(to);
}

The main part of the program. Read the number of vertices $n$ and edges $m$ in the graph.

scanf("%d %d", &n, &m);

Set the size of arrays $g$ and $u se d$ .

g.resize(n + 1);
used.resize(n + 1);

Read the list of edges. Construct the adjacency list.

for (int i = 0; i < m; i++)
{
  scanf("%d %d", &a, &b);
  g[a].push_back(b);
  g[b].push_back(a);
}

Read vertex $v$ and start a depth-first search from it.

scanf("%d", &v);
dfs(v);
printf("\n");

Java realization — adjacency matrix

import java.util.*;

public class Main
{
  static int g[][], used[];
  static int n, m;
  
  static void dfs(int v)
  {
    System.out.printf(v + " ");	  
    used[v] = 1;
    for(int i = 1; i <= n; i++) 
      if (g[v][i] == 1 && used[i] == 0) dfs(i);
  }
  
  public static void main(String[] args)
  {
    Scanner con = new Scanner(System.in);
    n = con.nextInt();
    m = con.nextInt();
    g = new int[n+1][n+1];
    used = new int[n+1];

    for (int i = 0; i < m; i++)
    {
      int a = con.nextInt();
      int b = con.nextInt();      
      g[a][b] = g[b][a] = 1;
    }
    
    int v = con.nextInt();    
    dfs(v);
    System.out.println();    
  }
}

Java realization — array of ArrayList

import java.util.*;

public class Main
{
  static ArrayList<Integer>[] g;	
  static int used[];
  static int n, m;
  
  static void dfs(int v)
  {
    System.out.print(v + " ");	  
    used[v] = 1;
    for(int to : g[v])
      if (used[to] == 0) dfs(to);
  }
  
  public static void main(String[] args)
  {
    Scanner con = new Scanner(System.in);
    n = con.nextInt();
    m = con.nextInt();
    g = new ArrayList[n+1]; // unchecked
    used = new int[n+1];

    for (int i = 1; i <= n; i++)
      g[i] = new ArrayList<Integer>();

    for (int i = 0; i < m; i++)
    {
      int a = con.nextInt();
      int b = con.nextInt();      
      g[a].add(b);
      g[b].add(a);
    }
    
    int v = con.nextInt();    
    dfs(v);
    System.out.println();    

    con.close();
  }
}

Java realization — ArrayList of ArrayList

import java.util.*;

public class Main
{
  static ArrayList<ArrayList<Integer>> g;	
  static int used[];
  static int n, m;
  
  static void dfs(int v)
  {
    System.out.printf(v + " ");	  
    used[v] = 1;
    for(int i = 0; i < g.get(v).size(); i++)
    {
      int to = g.get(v).get(i);
      if (used[to] == 0) dfs(to);
    }
  }
  
  public static void main(String[] args)
  {
    Scanner con = new Scanner(System.in);
    n = con.nextInt();
    m = con.nextInt();
    g = new ArrayList<ArrayList<Integer>>();
    used = new int[n+1];

    for (int i = 0; i <= n; i++)
      g.add(new ArrayList<Integer>());

    for (int i = 0; i < m; i++)
    {
      int a = con.nextInt();
      int b = con.nextInt();      
      g.get(a).add(b);
      g.get(b).add(a);
    }
    
    int v = con.nextInt();    
    dfs(v);
    System.out.println();    

    con.close();
  }
}

Python realization

The dfs function performs a depth-first search from vertex $v$ .

def dfs(v):

Print the vertex $v$ .

  print(v, end = ' ')

Mark the vertex $v$ as visited.

  used[v] = True

The list $g [v]$ contains the numbers of vertices adjacent to $v$ . Iterate over the vertices $t o$ that can be reached from $v$ . It's possible to go to vertex $t o$ from $v$ if vertex $t o$ is not visited $(u se d [t o] = 0)$ .

  for to in g[v]:
    if not used[to]: dfs(to)

The main part of the program. Read the number of vertices $n$ and edges $m$ in the graph.

n, m = map(int, input().split())

Create the adjacency list $g$ and the list $u se d$ .

g = [[] for _ in range(n+1)]
used = [False] * (n + 1)

Read the list of edges. Construct the adjacency list.

for _ in range(m):
  a, b = map(int, input().split())
  g[a].append(b)
  g[b].append(a)

Read vertex $v$ and start a depth-first search from it.

v = int(input())
dfs(v)