Розбір
Let be the input array of numbers. Initialize the pointers at the beginning of the array and at the end of the array. We will count the strength of the sequence in the variable . Initially, set .
While the pointers and do not meet, perform the following actions:
Move the pointer one position to the right if it does not point to the number .
Move the pointer one position to the left if it does not point to the number .
If both pointers point to the number , increase by one and move each pointer one position in the corresponding direction.
After the algorithm completes, the answer will be the value .
Example
Consider the second test. Initialize the pointers. Move the pointer to the right and the pointer to the left until they both point to the number .
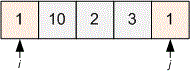
Move the pointer to the right and the pointer to the left until they both point to the number .

The pointers meet, we stop the algorithm. The answer will be the value .
Algorithm realization
Read the input data.
scanf("%d", &n);
v.resize(n);
for (i = 0; i < n; i++)
scanf("%d", &v[i]);Set the pointers to the start and end of the array .
int i = 0, j = v.size() - 1;
In the variable , we count the strength of the sequence.
k = 1;
while (i <= j)
{Move the pointer to the right until it encounters the number .
if (v[i] != k) i++;
Move the pointer to the left until it encounters the number .
if (v[j] != k) j--;
If both pointers point to the number , then increase by one.
if (v[i] == k && v[j] == k) k++; }
Print the answer.
printf("%d\n", k - 1);Python realization
Read the input data.
n = int(input()) v = list(map(int, input().split()))
Set the pointers to the start and end of the list .
i, j = 0, len(v) – 1
In the variable , we count the strength of the sequence.
k = 1 while i <= j:
Move the pointer to the right until it encounters the number .
if v[i] != k:
i += 1Move the pointer to the left until it encounters the number .
if v[j] != k:
j -= 1If both pointers point to the number , then increase by one.
if v[i] == k and v[j] == k:
k += 1Print the answer.
print(k - 1)