•Статьи•6 месяцев назад

Биномиальный коэффициент

Сочетанием из $n$ элементов по $k$ называется набор из $k$ элементов, выбранных из заданных $n$ элементов. При этом наборы, которые отличаются только порядком следования элементов (но не составом), считаются одинаковыми. Именно благодаря этому свойству сочетаний они отличаются от размещений.

Например, рассмотрим множество из $5$ элементов: ${1, 2, 3, 4, 5}$ . Наборы ${2, 1, 3}$ и ${3, 2, 1}$ являются одинаковыми как сочетания (хотя различны как размещения), поскольку составлены из тех же самых элементов ${1, 2, 3}$ .

Формула для вычисления количества сочетаний из $n$ по $k$ равна

C_{n}^{k} = \frac{n !}{k ! \cdot ( n - k )!}

Числа $C_{n}^{k}$ называются биномиальными коэффициентами.

Когда мы выбираем ноль элементов из множества из $n$ элементов, мы фактически делаем “пустой” выбор. Пустое множество, в данном контексте, считается допустимым сочетанием. Представьте, что у вас есть коробка с $n$ шарами, и вы хотите выбрать $0$ из них. Даже если Вы ничего не выбираете, это всё равно является допустимым вариантом выбора. Таким образом, $C_{n}^{0}$ означает количество способов выбрать $0$ элементов из $n$ , что равно $1$ .

Мы можем рассматривать это как один единственный способ не выбирать ни один элемент из множества, что и дает результат $1$ .

C_{n}^{0} = \frac{n !}{0 ! \cdot ( n - 0 )!} = \frac{n !}{1 ! \cdot n !} = 1

Когда мы выбираем один элемент из множества из $n$ элементов, у нас есть $n$ вариантов выбора: мы можем выбрать любой из $n$ элементов. Например, если у нас есть множество из чисел от $1$ до $5$ ( ${1, 2, 3, 4, 5}$ ), то мы можем выбрать одно число из этого множества, и у нас есть $5$ вариантов для этого выбора.

Значение $C_{n}^{1}$ равно $n$ , потому что есть $n$ способов выбрать один элемент из множества из $n$ элементов.

C_{n}^{1} = \frac{n !}{1 ! \cdot ( n - 1 )!} = n

При выборе $2$ элементов из $n$ — элементного множества, мы формируем комбинации пар. Для построения такой пары мы сначала выбираем один элемент, а затем второй.

Первый элемент можно выбрать из $n$ элементов.
После выбора первого элемента, у нас остается $n -1$ элемент для выбора второго элемента (поскольку мы не можем выбрать повторно тот же элемент).

Таким образом, общее количество комбинаций пар элементов, которые можно выбрать из $n$ — элементного множества, равно произведению числа способов выбрать первый и второй элементы: $n \cdot (n -1)$ .

Однако, каждая пара учтена дважды, так как порядок элементов в паре не имеет значения. Например, $(p, q)$ и $(q, p)$ считаются одной и той же парой. Чтобы учесть это, следует разделить общее количество комбинаций на $2$ . Таким образом, $C_{n}^{2}$ равно $n \cdot (n -1) /2$ .

C_{n}^{2} = \frac{n !}{2 ! \cdot ( n - 2 )!} = \frac{n \cdot ( n - 1 )}{2}

Свойство симметрии: $C_{n}^{k} = C_{n}^{n - k}$ .

Количество способов выбрать $k$ элементов из $n$ равно количеству способов не выбрать $(n - k)$ элементов из $n$ . Но не выбрать $(n - k)$ элементов из $n$ мы можем $C_{n}^{n - k}$ способами. Следовательно $C_{n}^{k} = C_{n}^{n - k}$ .

Упражнение. Вычислить значения следующих биномиальных коэффициентов:

1) $C_{5}^{2}$	3) $C_{5}^{4}$	5) $C_{8}^{1}$
2) $C_{8}^{3}$	4) $C_{7}^{5}$	6) $C_{8}^{5}$

Формула сложения: $C_{n}^{k} = C_{n - 1}^{k - 1} + C_{n - 1}^{k}$ .

Доказательство. Вычислим значение правой части равенства:

C_{n - 1}^{k - 1} + C_{n - 1}^{k} = \frac{( n - 1 )!}{( k - 1 )! \cdot ( n - k )!} + \frac{( n - 1 )!}{k ! \cdot ( n - k - 1 )!} =

\frac{( n - 1 )! \cdot k + ( n - 1 )! \cdot ( n - k )}{k ! \cdot ( n - k )!} = \frac{( n - 1 )! \cdot ( k + n - k )}{k ! \cdot ( n - k )!} = \frac{n !}{k ! \cdot ( n - k )!} = C_{n}^{k}

Готовясь к экзамену по математическому анализу, Петя разложил перед собой $n$ разных шпаргалок. Они были его спасением, ведь за весь семестр Петя так ни разу не удосужился учить материал как следует. Шпаргалок оказалось настолько много, что они не вмещались ни в один карман. Поэтому Петя решил подсчитать максимальное количество шпаргалок, которое он сможет взять с собой на экзамен. И тут возник вопрос: а сколько вообще существует способов выбрать нужное количество шпаргалок?

Входные данные. Содержит общее количество шпаргалок $n (1 \leq n \leq 12)$ и количество шпаргалок $k (0 \leq k \leq n)$ , которое Петя может взять с собой.

Выходные данные. Выведите количество способов выбрать $k$ шпаргалок из $n$ .

Открыть задачу

Биномиальные коэффициенты появляются в биноме Ньютона:

(x + y)^{n} = k = 0 \sum n C_{n}^{k} x^{k} y^{n - k}

Рассмотрим примеры:

(x + y)^{2} = C_{2}^{0} x^{2} y^{0} + C_{2}^{1} x^{1} y^{1} + C_{2}^{2} x^{0} y^{2} = x^{2} + 2 x y + y^{2},

(x + y)^{3} = C_{3}^{0} x^{3} y^{0} + C_{3}^{1} x^{2} y^{1} + C_{3}^{2} x^{1} y^{2} + C_{3}^{3} x^{0} y^{3} = x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3}

Рассмотрим $2 n$ объектов $a_{1}, ..., a_{2 n}$ и найдем количество способов выбрать $n$ объектов из $2 n$ .

Разобьём множество на две части: ${a_{1}, a_{2}, ..., a_{n}, a_{n + 1}, ..., a_{2 n}}$ . Чтобы выбрать $n$ объектов из $2 n$ , нам нужно выбрать $k (k \leq n)$ объектов из левой половины (то есть из множества ${a_{1}, a_{2}, ..., a_{n}})$ и $n - k$ объектов из правой (из множества ${a_{n + 1}, a_{n + 2}, ..., a_{2 n}})$ . Количество способов сделать такую выборку в соответствии с правилом умножения равно $C_{n}^{k} \cdot C_{n}^{n - k} = (C_{n}^{k})^{2}$ . Поскольку $k$ может принимать значения от $0$ до $n$ , то $\sum_{k = 0}^{n} (C_{n}^{k})^{2}$ равно количеству способов выбрать $n$ объектов из $2 n$ , то есть $C_{2 n}^{n}$ . Таким образом

(C_{n}^{0})^{2} + (C_{n}^{1})^{2} + (C_{n}^{2})^{2} + ... + (C_{n}^{n})^{2} = C_{2 n}^{n}

Пример

Для $n = 3$ ответ равен $(C_{3}^{0})^{2} + (C_{3}^{1})^{2} + (C_{3}^{2})^{2} + (C_{3}^{3})^{2} = 1^{2} + 3^{2} + 3^{2} + 1^{2} = 20$

В то же время $C_{6}^{3} = \frac{6 !}{3 ! \cdot 3 !} = \frac{4 \cdot 5 \cdot 6}{6} = 20$ .

Рассмотрим последовательность из $n$ единиц: $111...11$ . Между любыми двумя единицами можно вставить знак ‘ $+$ ’. Например $11 + 111 + 1$ . Такая запись будет обозначать сумму $2 + 3 + 1$ , где каждое слагаемое – количество единиц, стоящих рядом. Количество позиций, куда можно вставить знак ‘ $+$ ’, равно $n -1$ . Поскольку необходимо получить сумму из $k$ слагаемых, то следует вставить $k -1$ знак ‘ $+$ ’.

Нам следует вставить $k -1$ плюс на $n -1$ место. Это можно сделать $C_{n - 1}^{k - 1}$ способами.

Пример

Рассмотрим уравнение $x_{1} + x_{2} + x_{3} = 4$ . Оно имеет $3$ положительных целочисленных решения:

$(1, 1, 2)$
$(1, 2, 1)$
$(2, 1, 1)$

Например, $n = 4$ единицы на $k = 3$ слагаемых можно разбить $C_{2}^{3} = 3$ способами:

Рассмотрим последовательность из $n + k -1$ позиций. В $n$ позициях следует поставить $1$ . В $k -1$ позицию следует поставить символ ' $+$ ' (чтобы получить $k$ слагаемых).

Любой расстановке единиц и знаков ' $+$ ' по позициям будет соответствовать некоторое решение заданного уравнения. Например, рассмотрим некоторые решения уравнения $x_{1} + x_{2} + x_{3} = 4 (4$ единицы и $2$ плюса):

Нам следует вставить $k -1$ плюс на $n + k -1$ позиций. Это можно сделать $C_{n + k - 1}^{k - 1}$ способами.

Пример

Рассмотрим уравнение $x_{1} + x_{2} + x_{3} = 4$ . Его решениями будут:

$(4, 0, 0)$ и ее $3$ перестановки
$(3, 1, 0)$ и ее $6$ перестановок
$(2, 2, 0)$ и ее $3$ перестановки
$(2, 1, 1)$ и ее $3$ перестановки

Всего имеется $3 + 6 + 3 + 3 = 15$ решений.

Пусть $n$ — целое неотрицательное число. Обозначим

n! = 1 \cdot 2 \cdot ... \cdot n (0! = 1),

C_{n}^{k} = \frac{n !}{k ! \cdot ( n - k )!} (0 \leq k \leq n)

Для заданных $n$ и $k$ вычислите значение $C_{n}^{k}$ .

Входные данные. Первая строка содержит количество тестов $t (t \leq 50)$ . Каждая из следующих $t$ строк содержит два целых числа $n$ и $k (0 \leq n < 2^{64}, 0 \leq C_{n}^{k} < 2^{64})$ .

Выходные данные. Выведите $t$ строк, каждая из которых содержит значение $C_{n}^{k}$ для соответствующего теста.

Открыть задачу

Вычисления будем проводить с использованием $64$ -разрядных беззнаковых целых чисел (unsigned long long). Очевидно, что

C_{n}^{k} = \frac{n !}{k ! \cdot ( n - k )!} = \frac{n \cdot ( n - 1 ) \cdot ( n - 2 ) \cdot ... \cdot ( n - k + 1 )}{1 \cdot 2 \cdot 3 \cdot ... \cdot k} = \frac{n}{1} \cdot \frac{n - 1}{2} \cdot \frac{n - 2}{3} \cdot ... \cdot \frac{n - k + 1}{k}

Присвоим переменной $res$ значение $1$ , после чего будем ее умножать на $\frac{n - i + 1}{i}$ для всех $i$ от $1$ до $k$ . Каждый раз деление на $i$ будет целочисленным, однако при умножении можно получить переполнение. Пусть $d = НОД (res, i)$ . Тогда операцию

res = res * (n - i + 1) / i

перепишем через

res = (res / d) * ((n - i + 1) / (i / d))

При такой реализации переполнения при умножении не произойдет (ответ является $64$ -разрядным беззнаковым целым числом). Заметим, что сначала следует выполнить деление $(n - i + 1) / (i / d)$ , а потом умножение $res / d$ на полученное частное.

Для вычисления $C_{n}^{k}$ следует выполнить $k$ итераций. Но что делать, если следует вычислить $C_{2000000000}^{1999999999}$ ? Ответ не превысит $2^{64}$ , поэтому такие входные данные возможны. Поскольку $C_{n}^{k} = C_{n}^{n - k}$ , то при $n - k < k$ следует положить $k = n - k$ .

Пример

Рассмотрим следующий пример:

C_{6}^{3} = \frac{6}{1} \cdot \frac{5}{2} \cdot \frac{4}{3} = 15 \cdot \frac{4}{3}

Пусть $res = 15$ , и осталось выполнить умножение $res \cdot \frac{4}{3} = 15 * \frac{4}{3}$ . Вычислим $d = НОД (15, 3) = 3$ . Поэтому $15 \cdot \frac{4}{3} = (15/3) \cdot \frac{4}{3/3} = 5 \cdot \frac{4}{1} = 20$ .

Функция gcd вычисляет наибольший общий делитель чисел $a$ и $b$ .

unsigned long long gcd(unsigned long long a, unsigned long long b)
{
  return (!b) ? a : gcd(b,a % b);
}

Функция Cnk вычисляет значение биномиального коэффициента $C_{n}^{k}$ .

unsigned long long Cnk(unsigned long long n, unsigned long long k)
{
  unsigned long long CnkRes = 1, t, i;
  if (k > n - k) k = n - k;
  for(i = 1; i <= k; i++)
  {
    t = gcd(CnkRes, i);
    CnkRes = (CnkRes / t) * ((n - i + 1) / (i / t));
  }
  return CnkRes;
}

Основная часть программы. Читаем входные данные. Последовательно обрабатываем тесты.

scanf("%d",&t);
while(t--)
{
  scanf("%llu %llu",&n,&k);
  res = Cnk(n,k);
  printf("%llu\n",res);
}

Перепишем заданную сумму в виде:

1 \cdot C_{n}^{0} + 2 \cdot C_{n}^{1} + 3 \cdot C_{n}^{2} + ... + (n + 1) \cdot C_{n}^{n} =

(C_{n}^{0} + C_{n}^{1} + C_{n}^{2} + ... + C_{n}^{n}) + 1 \cdot C_{n}^{1} + 2 \cdot C_{n}^{2} + ... + n \cdot C_{n}^{n}

Сумма в скобках равна $2^{n}$ . Если в формуле бинома Ньютона

(a + b)^{n} = i = 0 \sum n C_{n}^{i} a^{i} b^{n - i}

положить $a = b = 1$ , то получим соотношение: $(1 + 1)^{n} = \sum_{i = 0}^{n} C_{n}^{i} 1^{i} 1^{n - i}$ , или

2^{n} = i = 0 \sum n C_{n}^{i} = C_{n}^{0} + C_{n}^{1} + ... + C_{n}^{n}

Вычислим оставшуюся сумму:

1 \cdot C_{n}^{1} + 2 \cdot C_{n}^{2} + ... + n \cdot C_{n}^{n} =

1 \cdot \frac{n !}{1 ! \cdot ( n - 1 )!} + 2 \cdot \frac{n !}{2 ! \cdot ( n - 2 )!} + ... + n \cdot \frac{n !}{n ! \cdot ( n - n )!} =

n \cdot (\frac{( n - 1 )!}{0 ! \cdot ( n - 1 )!} + \frac{( n - 1 )!}{1 ! \cdot ( n - 2 )!} + ... + \frac{( n - 1 )!}{( n - 1 )! \cdot ( n - n )!}) =

n \cdot (C_{n - 1}^{0} + C_{n - 1}^{1} + ... + C_{n - 1}^{n - 1}) = n \cdot 2^{n - 1}

Таким образом, ответ равен $2^{n} + n \cdot 2^{n - 1} = (n + 2) \cdot 2^{n - 1}$ .

Пример

Вычислим ответ для $n = 3$ . При непосредственном вычислении:

1 \cdot C_{3}^{0} + 2 \cdot C_{3}^{1} + 3 \cdot C_{3}^{2} + 4 \cdot C_{3}^{3} = 1 \cdot 1 + 2 \cdot 3 + 3 \cdot 3 + 4 \cdot 1 = 1 + 6 + 9 + 4 = 20

При вычислении по формуле: $5 \cdot 2^{2} = 20$ .

Читаем входное значение $n$ .

scanf("%lld", &n);

Вычисляем и выводим ответ.

res = (1LL << (n - 1)) * (n + 2);
printf("%lld\n", res);

Реализация алгоритма – функция

Объявим массив для запоминания результатов: $d p [n] [k] = C_{n}^{k}$ .

int dp[31][31];

Функия Cnk вычисляет значение биномиального коэффициента $C_{n}^{k}$ .

int Cnk(int n, int k)
{
  if (n == k) return 1;
  if (k == 0) return 1;
  if (dp[n][k] != -1) return dp[n][k];
  return dp[n][k] = (Cnk(n - 1, k - 1) + Cnk(n - 1, k)) % 9929;
}

Основная часть программы. Читаем входное значение $n$ .

scanf("%d", &n);
memset(dp, -1, sizeof(dp));

Вычисляем указанную сумму.

res = 0;
for (i = 0; i <= n; i++)
  res += (i + 1) * Cnk(n, i);

Выводим ответ.

printf("%d\n", res);

У Вас есть лист бумаги, и Вы выбираете на нем прямоугольник размером $n \cdot m$ . Назовем этот прямоугольник вместе с линиями, на которых он находится, сеткой. Начиная с левого нижнего угла сетки, Вы перемещаете карандаш в правый верхний угол, следя за тем, чтобы он оставался на линиях и двигался только вправо или вверх. Результат показан слева:

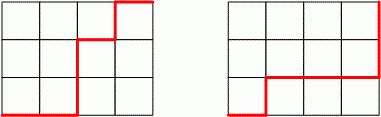
Действительно шедевр, не так ли? Повторяя процедуру еще раз, Вы получите картинку, показанную справа. Теперь возникает вопрос: сколько разных произведений искусства можно таким образом создать?

Входные данные. Два натуральных числа $n$ и $m$ .

Выходные данные. Выведите количество различных произведений искусства, которые можно создать, используя описанную выше процедуру. Можно утверждать, что это число соответствует $64$ — битовому знаковому целому числу.

Открыть задачу

Гуннар — достаточно старый и забывчивый исследователь. Сейчас он пишет статью о безопасности в социальных сетях, которая включает в себя некоторые элементы комбинаторики. Он написал программу для вычисления биномиальных коэффициентов, чтобы проверить некоторые расчеты.

Биномиальный коэффициент $C_{n}^{k}$ — это число

C_{n}^{k} = \frac{n !}{k ! \cdot ( n - k )!}

где $n$ и $k$ — неотрицательные числа.

Гуннар использует свою программу для вычисления $C_{n}^{k}$ и получил число $m$ в качестве результата. К несчастью, поскольку он забывчивый, он забыл числа $n$ и $k$ , которые он использовал в качестве входных данных. Эти два числа были результатом долгих вычислений, и они были записаны на одном из многочисленных листков, лежащих на его столе. Вместо того чтобы поискать в бумагах, он решил восстановить числа $n$ и $k$ по полученному ответу. Можете ли Вы помочь ему найти все такие возможные значения?

Входные данные. Первая строка содержит количество тестов, не большее $100$ . Каждый тест задается в одной строке и содержит целое число $m (2 \leq m \leq 1 0^{15})$ — результат программы Гуннара.

Выходные данные. Для каждого теста выведите две строки. Первая строка должна содержать количество способов выразить $m$ при помощи биномиального коэффициента. Во второй строке должны располагаться все пары $(n, k)$ , удовлетворяющие $C_{n}^{k} = m$ . Пары следует расположить по возрастанию $n$ , а в случае равенства по возрастанию $k$ . Формат вывода пар приведен в примере.

Открыть задачу

Если $C_{n}^{k} = m$ , то $C_{n}^{n - k} = m$ . Достаточно найти решение $k \leq n /2$ и вместе с парой $(k, n)$ вывести также пару $(k, n - k)$ . При $k = n /2$ эти две пары совпадают.

Пусть $p$ — наименьшее число, для которого $C_{2 p}^{p} > m$ . Тогда очевидно что $0 \leq k < p$ .

Зафиксируем такое $k$ что $C_{2 k}^{k} \leq m$ и рассмотрим функцию $f (n) = C_{n}^{k}$ . Тогда при $2 k \leq n \leq m$ функция $f (n)$ является монотонно возрастающей. Следовательно можно решить уравнение $f (n) = m$ бинарным поиском.

Таким образом для решения задачи следует перебрать значения $k (0 \leq k < p)$ и для каждого такого $k$ решить уравнение $C_{n}^{k} = m$ относительно $n$ бинарным поиском. Найденное значение $n$ должно быть целочисленным.

Пример

Рассмотрим уравнение $C_{n}^{k} = 3003$ . Учитывая что $C_{12}^{6} = 924$ , а $C_{14}^{7} = 3432$ , то нам достаточно перебрать $0 \leq k \leq 6$ .

Пусть $k = 2$ , рассмотрим уравнение $C_{n}^{2} = 3003$ или $\frac{n \cdot ( n - 1 )}{2} = 3003$ , $n \cdot (n -1) = 6006$ . Бинарным поиском в промежутке $4 \leq n \leq 3003$ находим целочисленное решение $n = 78$ . Учитывая что $n \neq = 2 \cdot k$ , имеем два решения: $C_{78}^{2} = C_{78}^{76} = 3003$ .

Искомые пары будем хранить в векторе пар $res$ .

vector<pair<long long,long long> > res;

Функция Cnk вычисляет значение биномиального коэффициента $C_{n}^{k}$ .

long long Cnk(long long n, long long k)
{
  long long i, Res = 1;
  if (k > n - k) k = n - k;
  for(i = 1; i <= k; i++)
  {

Если на очередной итерации результат превосходит $m$ (мы ищем решение уравнения $C_{n}^{k} = m$ ), то останавливаемся. Таким выходом из функции мы также избежим переполнения.

    if (1.0 * Res * (n - i + 1) / i > m) return m + 1;
    Res = Res * (n - i + 1) / i;
  }
  return Res;
}

Основная часть программы. Читаем входные данные.

scanf("%d",&tests);
while (tests--) 
{
  res.clear();
  scanf("%lld",&m);

Перебираем значение $k$ от $0$ до тех пор пока $C_{2 k}^{k} \leq m$ .

  for(k = 0; Cnk(2*k,k) <= m; k++)
  {

Ищем значение $n (2 k \leq n \leq m)$ бинарным поиском.

    long long lo = 2*k, hi = m;
    while (lo < hi) 
    {
      long long n = (lo + hi) / 2;
      if (Cnk(n,k) < m) lo = n + 1; else hi = n;
    }

Если $C_{l o}^{k} = m$ , то решение найдено. Заносим в результат одну или две пары решений.

    if (Cnk(lo,k) == m)
    {
      res.push_back(make_pair(lo,k));
      if (lo != 2*k)
        res.push_back(make_pair(lo,lo - k));
    }
  }

Сортируем пары.

  sort(res.begin(),res.end());

Выводим ответ — количество найденных пар и сами пары.

  printf("%d\n",res.size());
  for(i = 0; i < res.size(); i++)
    printf("(%lld,%lld) ", res[i].first,res[i].second);
  printf("\n");
}

Асимптотические оценки для Биномиального коэффициента

Теорема 1. Между биномиальными коэффициентами имеет место соотношение:

C_{n}^{0} < C_{n}^{1} < ... < C_{n}^{⌊ n /2 ⌋} \geq C_{n}^{⌊ n /2 ⌋ + 1} > ... > C_{n}^{n}

Теорема 2. $C_{2 n}^{n} < 4^{n}$ . Следует из того, что $\sum_{k = 0}^{2 n} C_{2 n}^{k} = (1 + 1)^{2 n} = 2^{2 n} = 4^{n}$

Теорема 3. $C_{2 n}^{n} > \frac{4 ^{n}}{2 n + 1}$ . Следует из того, что $\sum_{k = 0}^{2 n} C_{2 n}^{k} = 4^{n}$ , а самих коэффициентов $2 n + 1$ . Поэтому больший из коэффициентов будет больше $\frac{4 ^{n}}{2 n + 1}$ .

Теорема 4. Формула Стирлинга. $n! \approx 2 πn (\frac{n}{e})^{n}$ .

Более точное приближение имеет вид:

n! \approx 2 πn (\frac{n}{e})^{n} (1 + \frac{1}{12 n} + \frac{1}{288 n ^{2}} - \frac{139}{51849 n ^{3}} - \frac{571}{2488320 n ^{4}})

Теорема 5.

C_{2 n}^{n} \approx \frac{4 πn ( \frac{2 n}{e} ) ^{2 n}}{( 2 πn ( \frac{n}{e} ) ^{n} ) ^{2}} = \frac{4 ^{n}}{πn}

Теорема 6.

C_{n}^{k} = \frac{n !}{k ! ( n - k )!} = \frac{n \cdot ( n - 1 ) \cdot ( n - 2 ) \cdot ... \cdot ( n - k + 1 )}{1 \cdot 2 \cdot 3 \cdot ... \cdot k} =

\frac{n !}{k !} \cdot (1 - \frac{1}{n}) \cdot (1 - \frac{2}{n}) \cdot ... \cdot (1 - \frac{k - 1}{n}) =

\frac{n !}{k !} \cdot e^{l n (1 - \frac{1}{n}) + l n (1 - \frac{2}{n}) + ... + l n (1 - \frac{k - 1}{n})} \leq (воспользуемся неравенством l n (1 - x) \leq - x)

\frac{n !}{k !} \cdot e^{- \frac{1}{n} - \frac{2}{n} - ... - \frac{k - 1}{n}} = \frac{n !}{k !} \cdot e^{- \frac{k \cdot ( k - 1 )}{2 n}}

Список использованных задач

Комментарии

Пока ничего

Станьте первым, кто начнёт обсуждение!

Войти

Загрузка

Минутку, получение данных с сервера