Разбор

Для каждой вершины $v$ вычислим количество вершин $sum[v]$ в поддереве, где она является корнем. Если $t{o}_1,t{o}_2,...,t{o}_k$ — сыновья вершины $v$, то

Если вершина $v$ является листом дерева, то $sum[v]=1$.

Пусть $dp[v]$ равно количеству спасенных вершин в поддереве с корнем $v$, если на данный момент вершина $v$ (и только она в поддереве) заражена.

Если вершина $v$ имеет только одного сына $to$, то $dp[v]=sum[to]-1$ (удаленная вершина $to$ не является спасенной).

Пусть вершина $v$ имеет двух сыновей $t{o}_1$ и $t{o}_2$ (каждая вершина имеет степень не больше $3$). Тогда у нас имеется два варианта:

• Удалить $t{o}_1$ и рекурсивно спасать вершины поддерева с корнем $t{o}_2$. Число спасенных вершин составит $sum[t{o}_1]-1+dp[t{o}_2]$.

• Удалить $t{o}_2$ и рекурсивно спасать вершины поддерева с корнем $t{o}_1$. Число спасенных вершин составит $sum[t{o}_2]-1+dp[t{o}_1]$.

Из двух вариантов следует выбрать тот, при котором количество спасенных вершин будет большим.

Рассмотрим процесс поиска в глубину, когда рассматривается ребро $(v,to)$.

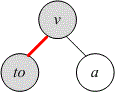
Пусть $a$ — второй сын вершины $v$. Нам следует вычислить значение $dp[to]+sum[a]-1$. Попробуем его найти, используя только вершины $v$ и $to$. Нам известно, что

Откуда

Следовательно

Перебираем сыновей $to$ вершины $v$ и вычисляем

Пример

В первом примере Хусейн сможет спасти две вершины $3$ и $4$, выбрав своим первым ходом вершину номер $2$.

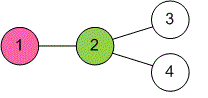
Рассмотрим второй пример. Возле каждой вершины $v$ поставим метки $sum[v]/dp[v]$. Вершины, выбранные Хусейном, отобразим зеленым цветом.

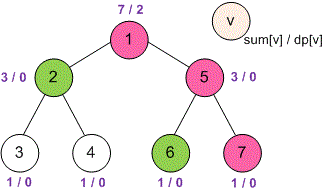
Например,

Реализация алгоритма

Объявим рабочие массивы.

#define MAX 300005
int sum[MAX], dp[MAX];
vector<vector<int>> g;

Функция dfs совершает поиск в глубину из вершины $v$. Предком вершины $v$ является $p$.

void dfs(int v, int p = -1)
{

Инициализируем значения $sum[v]$ и $dp[v]$.

  sum[v] = 1;
  dp[v] = 0;

Запускаем поиск в глубину из сыновей вершины $v$.

  for (int to : g[v])
    if (to != p)
    {
      dfs(to, v);
      sum[v] += sum[to];
    }

Вычисляем значение $dp[v]$.

  for (int to : g[v])
    if (to != p)
    {
      dp[v] = max(dp[v], sum[to] - 1); // if 1 son
      dp[v] = max(dp[v], dp[to] + sum[v] - sum[to] - 2);
    }
}

Основная часть программы. Читаем входные данные.

scanf("%d", &n);
g.clear(); g.resize(n + 1);
memset(dp, 0, sizeof(dp));
memset(sum, 0, sizeof(sum));
for (i = 1; i < n; i++)
{
  scanf("%d %d", &u, &v);
  g[u].push_back(v);
  g[v].push_back(u);
}

Запускаем поиск в глубину из вершины $1$.

dfs(1);

Выводим ответ.

printf("%d\n", dp[1]);