Розбір

Let’s consider three permutations: $a,p$, and $q$. Let $I$ be the identity permutation. Consider the equation: $a(p(q(I)))=I$. From this, we get $p(q(I))=a^{-1}$. Using the fact that permutations are applied from right to left, this identity can be rewritten as: $p°q=a^{-1}$. Therefore, $q=p^{-1}°a^{-1}$.

Generate a random permutation $p$ that has no fixed points. Then, compute the permutation $q=p^{-1}°a^{-1}$ and check that it has no fixed points. The found permutations $p$ and $q$ are the required ones.

Example

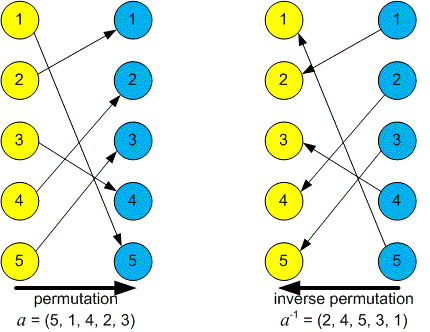
Consider the permutation $a=(5,1,4,2,3)$.

Its inverse will be $a^{-1}=(2,4,5,3,1)$.

Generate a random permutation $p$ with no fixed points. For example, let $p=(4,1,2,5,3)$. Now, let's compute its inverse: $p^{-1}=(2,3,5,1,4)$.

Next, compute $q=p^{-1}°a^{-1}=(2,3,5,1,4)°(2,4,5,3,1)=(3,1,4,5,2)$. The permutation $q$ has no fixed points, so it is valid.

Algorithm realization

The print function prints the elements of the array $a$, starting from the first one.

void print(vector<int>& a)
{
  for (int i = 1; i < a.size(); i++)
    printf("%d ", a[i]);
  printf("\n");
}

The function is_valid checks whether the permutation $v$ contains any fixed points.

bool is_valid(vector<int>& v)
{
  for (int i = 1; i < v.size(); i++)
    if (v[i] == i) return false;
  return true;
}

Declare the arrays.

vector<int> a, p, p1, q;

The main part of the program. Read the input data.

scanf("%d", &tests);
while (tests--)
{
  scanf("%d", &n);

Initialize the arrays.

  a.resize(n + 1);
  p1.resize(n + 1);
  p.resize(n + 1);
  q.resize(n + 1);

Read the input permutation $a$ and immediately store its inverse in the array $a$. That is, the array $a$ contains the permutation $a^{-1}$, where $a$ is the input permutation.

  for (i = 1; i <= n; i++)
  {
    scanf("%d", &x);
    a[x] = i;
  }

mt19937 is one of the standard pseudorandom number generators in C++ (Mersenne Twister with a period of 19937). It is very fast and has good statistical properties, making it an excellent choice for most tasks requiring random number generation.

  mt19937 gen(random_device{}());

In the variable $found$, we'll mark whether a solution is found for the current test.

  found = false;

Perform $1000$ iterations.

  for (it = 0; it < 1000; it++)
  {

Generate a random permutation. To do this, populate the array $p$ with the numbers $0,1,2,...$, and use the shuffle function to shuffle the elements, starting from the first (non-zero) element. We work with permutations from $1$ to $n$.

    iota(p.begin(), p.end(), 0);
    shuffle(p.begin() + 1, p.end(), gen);

Check whether the permutation $p$ is valid (i.e., it contains no fixed points).

    if (!is_valid(p)) continue;

Compute the permutation $p_1=p^{-1}$.

    for (i = 1; i <= n; i++)
      p1[p[i]] = i;

Compute the permutation $q=p_1°a^{-1}=p^{-1}°a^{-1}$.

    for (i = 1; i <= n; i++)
      q[i] = p1[a[i]];

If the permutation $q$ is valid, print the result.

    if (is_valid(q))
    {
      puts("Possible");
      print(p);
      print(q);
      found = true;
      break;
    }
  }

If no solution is found after $1000$ iterations, then no solution exists.

  if (!found) puts("Impossible");
}