Розбір

For each vertex $v$ , compute the number of vertices $s u m [v]$ in the subtree where it is the root. If $t o_{1}, t o_{2}, ..., t o_{k}$ are the children of vertex $v$ , then

s u m [v] = 1 + s u m [t o_{1}] + s u m [t o_{2}] + ... + s u m [t o_{k}]

If vertex $v$ is a leaf of the tree, then $s u m [v] = 1$ .

Let $d p [v]$ be the number of saved vertices in the subtree with root $v$ , assuming that currently vertex $v$ (and only it in the subtree) is infected.

If vertex $v$ has only one child $t o$ , then $d p [v] = s u m [t o] - 1$ (the removed vertex $t o$ is not considered saved).

Let vertex $v$ have two children $t o_{1}$ and $t o_{2}$ (each vertex has a degree of at most $3$ ). Then we have two options:

Remove $t o_{1}$ and recursively save the vertices in the subtree with root $t o_{2}$ . The number of saved vertices will be sum $s u m [t o_{1}] - 1 + d p [t o_{2}]$ .
Remove $t o_{2}$ and recursively save the vertices in the subtree with root $t o_{1}$ . The number of saved vertices will be $s u m [t o_{2}] - 1 + d p [t o_{1}]$ .

Among the two options, choose the one that maximizes the number of saved vertices.

Consider the depth-first search process when examining the edge $(v, t o)$ .

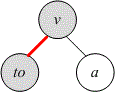
Let $a$ be the second child of vertex $v$ . We need to compute the value $d p [t o] + s u m [a] - 1$ . Let's try to find it using only the vertices $v$ and $t o$ . We know that:

s u m [v] = 1 + s u m [t o] + s u m [a]

From which it follows that:

s u m [a] = s u m [v] - s u m [t o] - 1

Thus,

d p [t o] + s u m [a] - 1 = d p [t o] + s u m [v] - s u m [t o] - 2

Iterate over the children $t o$ of the vertex $v$ and compute:

d p [v] = ma x (d p [t o] + s u m [v] - s u m [t o] - 2)

Example

In the first example, Huseyn is able to save two vertices, $3$ and $4$ , by choosing vertex number $2$ as his first move.|

Consider the second example. Next to each vertex $v$ , place the labels $s u m [v] / d p [v]$ . The vertices chosen by Huseyn are displayed in green.

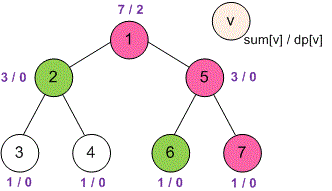
For example,

d p [1] = ma x (s u m [2] - 1 + d p [5], s u m [5] - 1 + d p [2]) = ma x (2, 2) = 2, s u m [1] = 1 + s u m [2] + s u m [5] = 1 + 3 + 3 = 7

Algorithm implementation

Declare the arrays.

#define MAX 300005
int sum[MAX], dp[MAX];
vector<vector<int>> g;

The function dfs performs a depth-first search starting from vertex $v$ . The parent of vertex $v$ is $p$ .

void dfs(int v, int p = -1)
{

Initialize the variables $s u m [v]$ and $d p [v]$ .

  sum[v] = 1;
  dp[v] = 0;

Perform a depth-first search starting from the children of vertex $v$ .

  for (int to : g[v])
    if (to != p)
    {
      dfs(to, v);
      sum[v] += sum[to];
    }

Compute the value of $d p [v]$ .

  for (int to : g[v])
    if (to != p)
    {
      dp[v] = max(dp[v], sum[to] - 1); // if 1 son
      dp[v] = max(dp[v], dp[to] + sum[v] - sum[to] - 2);
    }
}

The main part of the program. Read the input data.

scanf("%d", &n);
g.clear(); g.resize(n + 1);
memset(dp, 0, sizeof(dp));
memset(sum, 0, sizeof(sum));
for (i = 1; i < n; i++)
{
  scanf("%d %d", &u, &v);
  g[u].push_back(v);
  g[v].push_back(u);
}

Perform a depth-first search starting from vertex $1$ .

dfs(1);

Print the answer.

printf("%d\n", dp[1]);