•Article•10 ay öncə

Binomial əmsalı

Seçim $n$ elementdən $k$ elementin seçilməsidir, burada verilmiş $n$ elementdən $k$ elementi seçilir. Bu halda, elementlərin sıralanması fərqli olan dəstlər (lakin tərkibi fərqli olmayan) eyni hesab olunur. Seçimlərin bu xüsusiyyətinə görə onlar yerləşdirmələrdən fərqlənirlər.

Məsələn, $5$ elementdən ibarət olan çoxluğu nəzərdən keçirək: ${1, 2, 3, 4, 5}$ . ${2, 1, 3}$ və ${3, 2, 1}$ dəstləri seçim olaraq eyni hesab olunur (yerdəyişmə olaraq fərqli olsalar da), çünki eyni elementlərdən ${1, 2, 3}$ ibarətdir.

$n$ -dən $k$ -yə qədər seçimlərin sayının hesablanması üçün formula belədir

C_{n}^{k} = \frac{n !}{k ! \cdot ( n - k )!}

$C_{n}^{k}$ ədədləri binomial əmsallar adlanır.

$n$ elementdən ibarət olan çoxluqdan sıfır element seçdiyimiz zaman əslində "boş" seçim edirik. Bu kontekstdə boş çoxluq düzgün seçim hesab olunur. Təsəvvür edin ki, $n$ topları olan bir qutunuz var və onlardan $0$ ədədini seçmək istəyirsiniz. Heç bir şey seçməsəniz belə, bu yenə də düzgün seçim variantıdır. Beləliklə, $C_{n}^{0}$ $n$ -dən $0$ element seçmənin sayını bildirir ki, bu da $1$ -ə bərabərdir.

Bunu heç bir element seçməmək üçün yalnız bir yol kimi nəzərə ala bilərik ki, bu da nəticədə $1$ verir.

C_{n}^{0} = \frac{n !}{0 ! \cdot ( n - 0 )!} = \frac{n !}{1 ! \cdot n !} = 1

$n$ elementdən ibarət olan çoxluqdan bir element seçdiyimiz zaman $n$ seçmə variantımız var: $n$ elementdən istənilən birini seçə bilərik. Məsələn, $1$ -dən $5$ -ə qədər ədədlərdən ibarət olan çoxluqdan ( ${1, 2, 3, 4, 5}$ ) bir ədəd seçsək, bu çoxluqdan bir ədəd seçmək üçün $5$ variantımız var.

$C_{n}^{1}$ -in dəyəri $n$ -ə bərabərdir, çünki $n$ elementdən ibarət olan çoxluqdan bir elementi seçmənin $n$ yolu var.

C_{n}^{1} = \frac{n !}{1 ! \cdot ( n - 1 )!} = n

$n$ elementdən ibarət olan çoxluqdan $2$ element seçdiyimiz zaman cütlüklər təşkil edirik. Belə bir cütlüyün qurulması üçün əvvəlcə bir elementi, sonra isə ikinci elementi seçirik.

Birinci elementi $n$ elementdən seçə bilərik.
Birinci elementi seçdikdən sonra ikinci elementi seçmək üçün $n -1$ element qalır (çünki eyni elementi təkrarən seçə bilmərik).

Beləliklə, $n$ elementdən ibarət olan çoxluqdan cüt elementlərin seçilmə üsullarının ümumi sayı birinci və ikinci elementləri seçmənin yollarının hasilinə bərabərdir: $n \cdot (n -1)$ .

Lakin, hər bir cütlük iki dəfə sayılır, çünki cütlükdə elementlərin sırası əhəmiyyət daşımır. Məsələn, $(p, q)$ və $(q, p)$ eyni cütlük hesab olunur. Bunu nəzərə alaraq, cütlüklərin ümumi sayını $2$ -yə bölmək lazımdır. Beləliklə, $C_{n}^{2}$ $n \cdot (n -1) /2$ -yə bərabərdir.

C_{n}^{2} = \frac{n !}{2 ! \cdot ( n - 2 )!} = \frac{n \cdot ( n - 1 )}{2}

Simmetriya xüsusiyyəti: $C_{n}^{k} = C_{n}^{n - k}$ .

$n$ elementdən $k$ elementi seçmənin sayı $n$ elementdən $(n - k)$ elementi seçmənin sayına bərabərdir. Amma $n$ elementdən $(n - k)$ elementi seçmənin $C_{n}^{n - k}$ yolu var. Deməli, $C_{n}^{k} = C_{n}^{n - k}$ .

Tapşırıq. Aşağıdakı binomial əmsalların qiymətlərini hesablayın:

1) $C_{5}^{2}$	3) $C_{5}^{4}$	5) $C_{8}^{1}$
2) $C_{8}^{3}$	4) $C_{7}^{5}$	6) $C_{8}^{5}$

Yığma formulu: $C_{n}^{k} = C_{n - 1}^{k - 1} + C_{n - 1}^{k}$ .

İspat. Bərabərliyin sağ tərəfindəki dəyəri hesablayın:

C_{n - 1}^{k - 1} + C_{n - 1}^{k} = \frac{( n - 1 )!}{( k - 1 )! \cdot ( n - k )!} + \frac{( n - 1 )!}{k ! \cdot ( n - k - 1 )!} =

\frac{( n - 1 )! \cdot k + ( n - 1 )! \cdot ( n - k )}{k ! \cdot ( n - k )!} = \frac{( n - 1 )! \cdot ( k + n - k )}{k ! \cdot ( n - k )!} = \frac{n !}{k ! \cdot ( n - k )!} = C_{n}^{k}

Riyazi analiz imtahanına hazırlaşarkən, Petyanın qarşısında $n$ müxtəlif yazıqlar var idi. Onlar onun xilas yolu idi, çünki bütün semestr boyunca Petya materialı düzgün öyr

ənməyə cəhd etməmişdi. Yazıqlar o qədər çox idi ki, onlar heç bir cibə yerləşmirdi. Buna görə Petya imtahana öz ilə götürə biləcəyi maksimum yazıq sayını hesablamağa qərar verdi. Və burada bir sual meydana çıxdı: ümumiyyətlə lazımi yazıqların sayını seçmənin neçə yolu var?

Giriş məlumatları. Ümumi yazıq sayı $n (1 \leq n \leq 12)$ və Petyanın özü ilə götürə biləcəyi yazıq sayı $k (0 \leq k \leq n)$ verilmişdir.

Çıxış məlumatları. $n$ yazıqdan $k$ yazıq seçmənin yollarının sayını çıxarın.

Məsələni aç

Binomial əmsallar Nyuton binomunda görünür:

(x + y)^{n} = k = 0 \sum n C_{n}^{k} x^{k} y^{n - k}

Nümunələri nəzərdən keçirək:

(x + y)^{2} = C_{2}^{0} x^{2} y^{0} + C_{2}^{1} x^{1} y^{1} + C_{2}^{2} x^{0} y^{2} = x^{2} + 2 x y + y^{2},

(x + y)^{3} = C_{3}^{0} x^{3} y^{0} + C_{3}^{1} x^{2} y^{1} + C_{3}^{2} x^{1} y^{2} + C_{3}^{3} x^{0} y^{3} = x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3}

$2 n$ obyektlərindən $a_{1}, ..., a_{2 n}$ -i nəzərdən keçirək və $2 n$ obyektlərindən $n$ obyektini seçmənin sayını tapın.

Çoxluğu iki hissəyə bölək: ${a_{1}, a_{2}, ..., a_{n}, a_{n + 1}, ..., a_{2 n}}$ . $2 n$ obyektlərindən $n$ obyektini seçmək üçün, sol yarıdan (yəni ${a_{1}, a_{2}, ..., a_{n}}$ çoxluğundan) $k (k \leq n)$ obyektini və sağ yarıdan $n - k$ obyektini seçmək lazımdır (yəni ${a_{n + 1}, a_{n + 2}, ..., a_{2 n}}$ çoxluğundan). Bu seçimi etmənin yollarının sayı vurma qaydasına görə $C_{n}^{k} \cdot C_{n}^{n - k} = (C_{n}^{k})^{2}$ -ə bərabərdir. $k$ $0$ -dan $n$ -ə qədər dəyişə bildiyi üçün $\sum_{k = 0}^{n} (C_{n}^{k})^{2}$ $2 n$ -dən $n$ -ə qədər seçmənin yollarının sayına bərabərdir, yəni $C_{2 n}^{n}$ . Beləliklə

(C_{n}^{0})^{2} + (C_{n}^{1})^{2} + (C_{n}^{2})^{2} + ... + (C_{n}^{n})^{2} = C_{2 n}^{n}

Nümunə

$n = 3$ üçün cavab belədir: $(C_{3}^{0})^{2} + (C_{3}^{1})^{2} + (C_{3}^{2})^{2} + (C_{3}^{3})^{2} = 1^{2} + 3^{2} + 3^{2} + 1^{2} = 20$

Eyni zamanda $C_{6}^{3} = \frac{6 !}{3 ! \cdot 3 !} = \frac{4 \cdot 5 \cdot 6}{6} = 20$ .

Hesablamalar $64$ bitlik işarəsiz tam ədədlərdən (unsigned long long) istifadə edilərək aparılacaq. Aydındır ki,

C_{n}^{k} = \frac{n !}{k ! \cdot ( n - k )!} = \frac{n \cdot ( n - 1 ) \cdot ( n - 2 ) \cdot ... \cdot ( n - k + 1 )}{1 \cdot 2 \cdot 3 \cdot ... \cdot k} = \frac{n}{1} \cdot \frac{n - 1}{2} \cdot n - 2 \cdot 3 \cdot ... \cdot \frac{n - k + 1}{k}

Dəyişən $res$ -ə $1$ qiyməti verin, sonra isə onu $i = 1$ -dən $k$ -yə qədər bütün $n - i + 1/ i$ -ə vurun. Hər dəfə bölmə tam ədədli olacaq, lakin vurma zamanı yüklənmə baş verə bilər. $d = res v ə i - nin ə nb \overset{o}{¨} y \overset{u}{¨} k or t a q b \overset{o}{¨} l ə ni$ olsun. Onda əməliyyat

res = res * (n - i + 1) / i

aşağıdakı kimi yazılsın

res = (res / d) * ((n - i + 1) / (i / d))

Bu tətbiqlə vurma zamanı yüklənmə baş verməyəcək (cavab $64$ bitlik işarəsiz tam ədəddir). Əvvəlcə $(n - i + 1) / (i / d)$ bölməsini, sonra isə $res / d$ -i əldə edilmiş qismətə vurmağı unutmayın.

$C_{n}^{k}$ -nı hesablamaq üçün $k$ iterasiya yerinə yetirmək lazımdır. Lakin $C_{2000000000}^{1999999999}$ -u hesablamaq lazım gələrsə nə etməli? Cavab $2^{64}$ -ü keçməyəcək, ona görə də belə giriş məlumatları mümkündür. $C_{n}^{k} = C_{n}^{n - k}$ olduğuna görə $n - k < k$ olduqda $k = n - k$ qəbul edilməlidir.

Nümunə

Aşağıdakı nümunəni nəzərdən keçirək:

C_{6}^{3} = \frac{6}{1} \cdot \frac{5}{2} \cdot \frac{4}{3} = 15 \cdot \frac{4}{3}

$15 * \frac{4}{3}$ vurması qalıb. $d = 15 v ə3 - \overset{u}{¨} n ə nb \overset{o}{¨} y \overset{u}{¨} k or t a q b \overset{o}{¨} l ə ni = 3$ . Buna görə $15 \cdot \frac{4}{3} = (15/3) \cdot \frac{4}{3/3} = 5 \cdot \frac{4}{1} = 20$ .

gcd funksiyası $a$ və $b$ ədədlərinin ən böyük ortaq bölənini hesablayır.

unsigned long long gcd(unsigned long long a, unsigned long long b)
{
  return (!b) ? a : gcd(b,a % b);
}

Cnk funksiyası binomial əmsalın qiymətini hesablayır.

unsigned long long Cnk(unsigned long long n, unsigned long long k)
{
  unsigned long long CnkRes = 1, t, i;
  if (k > n - k) k = n - k;
  for(i = 1; i <= k; i++)
  {

Növbəti iterasiyada nəticə $m$ -i keçərsə (məsələni həll etmək üçün $C_{n}^{k} = m$ tənliyini axtarırıq), dayanırıq. Bu funksiyadan çıxmaqla yüklənmədən də qaçırıq.

    if (1.0 * Res * (n - i + 1) / i > m) return m + 1;
    Res = Res * (n - i + 1) / i;
  }
  return Res;
}

Proqramın əsas hissəsi. Giriş məlumatlarını oxuyun.

scanf("%d",&t);
while(t--)
{
  scanf("%llu %llu",&n,&k);
  res = Cnk(n,k);
  printf("%llu\n",res);
}

Verilmiş cəmi aşağıdakı kimi yazın:

1 \cdot C_{n}^{0} + 2 \cdot C_{n}^{1} + 3 \cdot C_{n}^{2} + ... + (n + 1) \cdot C_{n}^{n} =

(C_{n}^{0} + C_{n}^{1} + C_{n}^{2} + ... + C_{n}^{n}) + 1 \cdot C_{n}^{1} + 2 \cdot C_{n}^{2} + ... + n \cdot C_{n}^{n}

Qövslərdə olan cəm $2^{n}$ -ə bərabərdir. Nyuton binomu formulasında

(a + b)^{n} = i = 0 \sum n C_{n}^{i} a^{i} b^{n - i}

$a = b = 1$ qəbul edildikdə, əlaqə belə görünəcək: $(1 + 1)^{n} = \sum_{i = 0}^{n} C_{n}^{i} 1^{i} 1^{n - i}$ , və ya

2^{n} = i = 0 \sum n C_{n}^{i} = C_{n}^{0} + C_{n}^{1} + ... + C_{n}^{n}

Qalan cəmi hesablayın:

1 \cdot C_{n}^{1} + 2 \cdot C_{n}^{2} + ... + n \cdot C_{n}^{n} =

1 \cdot \frac{n !}{1 ! \cdot ( n - 1 )!} + 2 \cdot \frac{n !}{2 ! \cdot ( n - 2 )!} + ... + n \cdot \frac{n !}{n ! \cdot ( n - n )!} =

n \cdot (\frac{( n - 1 )!}{0 ! \cdot ( n - 1 )!} + \frac{( n - 1 )!}{1 ! \cdot ( n - 2 )!} + ... + \frac{( n - 1 )!}{( n - 1 )! \cdot ( n - n )!}) =

n \cdot (C_{n - 1}^{0} + C_{n - 1}^{1} + ... + C_{n - 1}^{n - 1}) = n \cdot 2^{n - 1}

Beləliklə, cavab $2^{n} + n \cdot 2^{n - 1} = (n + 2) \cdot 2^{n - 1}$ -ə bərabərdir.

Nümunə

$n = 3$ üçün cavabı hesablayaq. Düzgün hesablama ilə:

1 \cdot C_{3}^{0} + 2 \cdot C_{3}^{1} + 3 \cdot C_{3}^{2} + 4 \cdot C_{3}^{3} = 1 \cdot 1 + 2 \cdot 3 + 3 \cdot 3 + 4 \cdot 1 = 1 + 6 + 9 + 4 = 20

Formula ilə hesablama zamanı: $5 \cdot 2^{2} = 20$ .

Sizdə bir parça kağız var və onda $n \cdot m$ ölçüsündə düzbucaqlı seçirsiniz. Bu düzbucaqlını, onun üzərində yerləşən xətlər ilə birlikdə, şəbəkə adlandıraq. Şəbəkənin sol alt küncündən başlayaraq, karandaşınızı sağ üst küncə hərəkət etdirirsiniz, xətlər üzərində qalaraq yalnız sağa və ya yuxarı hərəkət edirsiniz. Nəticə solda göstərilmişdir:

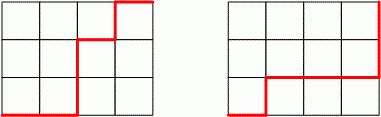
Həqiqətən bir şah əsər deyilmi? Proseduru yenidən təkrarlayaraq, sağda göstərilmiş şəkildə nəticə əldə edəcəksiniz. İndi isə sual yaranır: bu üsulla neçə fərqli sənət əsəri yaratmaq olar?

Giriş məlumatları. İki təbii ədəd $n$ və $m$ .

Çıxış məlumatları. Yuxarıda təsvir olunan prosedurdan istifadə edərək yaratmaq mümkün olan müxtəlif sənət əsərlərinin sayını çıxarın. Bu sayın $64$ bitlik işarəli tam ədədə uyğun gəldiyini deyə bilərik.

Məsələni aç

Gunnar kifayət qədər yaşlı və unutqan bir tədqiqatçıdır. Hazırda o, sosial şəbəkələrdə təhlükəsizlik mövzusunda məqalə yazır və bu məqalədə bəzi kombinatorika elementləri də yer alır. O, bəzi hesablamaları yoxlamaq üçün binomial əmsalların hesablanması üçün proqram yazıb.

Binomial əmsal $C_{n}^{k}$ bu ədəddir

C_{n}^{k} = \frac{n !}{k ! \cdot ( n - k )!}

$n$ və $k$ qeyri-mənfi ədədlərdir.

Gunnar proqramından istifadə edərək $C_{n}^{k}$ -ni hesablayıb və nəticədə $m$ ədədini alıb. Təəssüf ki, unutqan olduğuna görə, o, giriş kimi istifadə etdiyi $n$ və $k$ ədədlərini unudub. Bu iki ədəd uzun hesablamaların nəticəsi idi və onlar masasının üzərində olan çoxsaylı kağızlardan birində yazılmışdı. Kağızlarda axtarmaq əvəzinə, o, alınan cavabdan $n$ və $k$ ədədlərini bərpa etməyə qərar verdi. Ona bütün mümkün qiymətləri tapmaqda kömək edə bilərsinizmi?

Giriş məlumatları. Birinci sətir testlərin sayını, ən çox $100$ , ehtiva edir. Hər test bir sətirdə verilir və Gunnarın proqramının nəticəsi olan $m (2 \leq m \leq 1 0^{15})$ tam ədədini ehtiva edir.

Çıxış məlumatları. Hər test üçün iki sətir çap edin. Birinci sətir $m$ ədədini binomial əms

aldan ifadə etməyin üsullarının sayını ehtiva etməlidir. İkinci sətirdə $C_{n}^{k} = m$ şərtini ödəyən bütün $(n, k)$ cütləri olmalıdır. Cütlər $n$ artan sırası ilə və $k$ artan sırası ilə yerləşdirilməlidir. Cütlərin çap formatı nümunədə göstərilmişdir.

Məsələni aç

$C_{n}^{k} = m$ şərti yerinə yetirilərsə, onda $C_{n}^{n - k} = m$ şərti də yerinə yetirilir. $k \leq n /2$ həllini tapmaq və $(k, n)$ cütü ilə birlikdə $(k, n - k)$ cütünü də çıxarmaq kifayətdir. $k = n /2$ olduqda bu iki cüt eyni olur.

$p$ -ni $C_{2 p}^{p} > m$ olan ən kiçik ədəd qəbul edək. Onda $0 \leq k < p$ olduğu aydındır.

$k$ -ni sabitləşdirmək üçün $C_{2 k}^{k} \leq m$ və $f (n) = C_{n}^{k}$ funksiyasını nəzərdən keçirək. Onda $2 k \leq n \leq m$ aralığında $f (n)$ funksiyası artandır. Deməli, $f (n) = m$ tənliyini ikili axtarışla həll etmək olar.

Beləliklə, $k (0 \leq k < p)$ qiymətlərini nəzərdən keçirmək və hər belə $k$ üçün $C_{n}^{k} = m$ tənliyini ikili axtarışla həll etmək lazımdır. Tapılan $n$ dəyəri tam ədəd olmalıdır.

Nümunə

$C_{n}^{k} = 3003$ tənliyini nəzərdən keçirək. $C_{12}^{6} = 924$ , $C_{14}^{7} = 3432$ olduğuna görə, $0 \leq k \leq 6$ nəzərdən keçirmək kifayətdir.

$k = 2$ olduqda $C_{n}^{2} = 3003$ tənliyini və ya $\frac{n \cdot ( n - 1 )}{2} = 3003$ , $n \cdot (n -1) = 6006$ tənliyini nəzərdən keçirək. $4 \leq n \leq 3003$ aralığında ikili axtarışla tam həll $n = 78$ tapılır. $n \neq = 2 \cdot k$ olduğuna görə iki həll var: $C_{78}^{2} = C_{78}^{76} = 3003$ .

Axtarılan cütləri cütlər vektorunda saxlayaq.

vector<pair<long long,long long> > res;

Cnk funksiyası $C_{n}^{k}$ binomial əmsalının qiymətini hesablayır.

long long Cnk(long long n, long long k)
{
  long long i, Res = 1;
  if (k > n - k) k = n - k;
  for(i = 1; i <= k; i++)
  {

Növbəti iterasiyada nəticə $m$ -i keçərsə (məsələni həll etmək üçün $C_{n}^{k} = m$ tənliyini axtarırıq), dayanırıq. Bu funksiyadan çıxmaqla yüklənmədən də qaçırıq.

    if (1.0 * Res * (n - i + 1) / i > m) return m + 1;
    Res = Res * (n - i + 1) / i;
  }
  return Res;
}

Proqramın əsas hissəsi. Giriş məlumatlarını oxuyun.

scanf("%d",&tests);
while (tests--) 
{
  res.clear();
  scanf("%lld",&m);

$k$ dəyərini $C_{2 k}^{k} \leq m$ qədər nəzərdən keçirin.

  for(k = 0; Cnk(2*k,k) <= m; k++)
  {

$2 k \leq n \leq m$ aralığında $n$ dəyərini ikili axtarışla tapın.

    long long lo = 2*k, hi = m;
    while (lo < hi) 
    {
      long long n = (lo + hi) / 2;
      if (Cnk(n,k) < m) lo = n + 1; else hi = n;
    }

$C_{l o}^{k} = m$ olduqda həll tapılır. Nəticəyə bir və ya iki cüt həll daxil edin.

    if (Cnk(lo,k) == m)
    {
      res.push_back(make_pair(lo,k));
      if (lo != 2*k)
        res.push_back(make_pair(lo,lo - k));
    }
  }

Cütləri sırala.

  sort(res.begin(),res.end());

Cavabı çıxarın - tapılan cütlərin sayını və cütləri.

  printf("%d\n",res.size());
  for(i = 0; i < res.size(); i++)
    printf("(%lld,%lld) ", res[i].first,res[i].second);
  printf("\n");
}

Binomial əmsal üçün asimptotik qiymətləndirmələr

Teorema 1. Binomial əmsallar arasında belə bir əlaqə var:

C_{n}^{0} < C_{n}^{1} < ... < C_{n}^{⌊ n /2 ⌋} \geq C_{n}^{⌊ n /2 ⌋ + 1} > ... > C_{n}^{n}

Teorema 2. $C_{2 n}^{n} < 4^{n}$ . Bu ondan irəli gəlir ki, $\sum_{k = 0}^{2 n} C_{2 n}^{k} = (1 + 1)^{2 n} = 2^{2 n} = 4^{n}$

Teorema 3. $C_{2 n}^{n} > \frac{4 ^{n}}{2 n + 1}$ . Bu ondan irəli gəlir ki, $\sum_{k = 0}^{2 n} C_{2 n}^{k} = 4^{n}$ , və əmsallar $2 n + 1$ -dir. Buna görə daha böyük əmsal $\frac{4 ^{n}}{2 n + 1}$ -dən çox olacaq.

Teorema 4. Stirlinq formulu. $n! \approx 2 πn (\frac{n}{e})^{n}$ .

Daha dəqiq təxmini formulu:

n! \approx 2 πn (\frac{n}{e})^{n} (1 + \frac{1}{12 n} + \frac{1}{288 n ^{2}} - \frac{139}{51849 n ^{3}} - \frac{571}{2488320 n ^{4}})

Teorema 5.

C_{2 n}^{n} \approx \frac{4 πn ( \frac{2 n}{e} ) ^{2 n}}{( 2 πn ( \frac{n}{e} ) ^{n} ) ^{2}} = \frac{4 ^{n}}{πn}

Teorema 6.

C_{n}^{k} = \frac{n !}{k ! ( n - k )!} = \frac{n \cdot ( n - 1 ) \cdot ( n - 2 ) \cdot ... \cdot ( n - k + 1 )}{1 \cdot 2 \cdot 3 \cdot ... \cdot k} =

\frac{n !}{k !} \cdot (1 - \frac{1}{n}) \cdot (1 - \frac{2}{n}) \cdot ... \cdot (1 - \frac{k - 1}{n}) =

\frac{n !}{k !} \cdot e^{l n (1 - \frac{1}{n}) + l n (1 - \frac{2}{n}) + ... + l n (1 - \frac{k - 1}{n})} \leq (l n (1 - x) \leq - x n e q a l i v a s i t ə s i l ə)

\frac{n !}{k !} \cdot e^{- \frac{1}{n} - \frac{2}{n} - ... - \frac{k - 1}{n}} = \frac{n !}{k !} \cdot e^{- \frac{k \cdot ( k - 1 )}{2 n}}

İstifadə olunan məsələlərin siyahısı

Şərhlər

Yüklənir

Bir an, serverdən məlumat alınır